湖北省省直辖县级行政单位天门市九校联考2023-2024学年八年级上学期12月月考数学试题

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列式子一定成立的是（　　）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(- a)}^{2} · (- a^{3}) = - a^{5}$ C、 $a^{0} = 1$ D、 ${(- m^{3})}^{2} = m^{5}$

查看试题解析
2. 若 $2^{x} = 3, 4^{y} = 5$ 则 $2^{x + 2 y}$ 的值为（　　）

A、15 B、－2 C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{6}{5}$

查看试题解析
3. 如图，在△ABC中， $∠ B A C = 110 °$ ， MP和NQ分别垂直平分AB和AC ，则∠PAQ的度数是（　　）

A、20° B、40° C、50° D、60°

查看试题解析
4. 如图， $∠ A C B = 90 °$ ， $A C = B C$ ， BE⊥CE ， AD⊥CE于D点， $A D = 2.5 c m$ ， $D E = 1.7 c m$ ，则BE的长为（　　）

A、0.8 B、1 C、1.5 D、4.2

查看试题解析
5. 如图，折叠直角三角形纸片的直角，使点C落在AB上的点E处，已知BC=24，∠B=30°，则DE的长是（）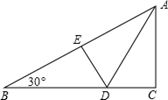

A、12 B、10 C、8 D、6

查看试题解析
6. 下列命题是真命题的是（　　）

A、等腰三角形的对称轴是底边上的中线； B、等腰三角形两腰上的中线不一定相等； C、线段有2条对称轴； D、有三条对称轴的三角形不一定是等边三角形.

查看试题解析
7. Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H ， EF⊥AB于F ，则下列结论中不正确的是（　　）

A、 $∠ A C D = ∠ B$ B、 $C H = C E = E F$ C、 $C H = H D$ D、 $A C = A F$

查看试题解析
8. 已知点A（4，3）和点B是平面内两点，且它们关于直线 $x = 3$ 轴对称，则点B的坐标为（　　）

A、（2，3） B、（-10，3） C、（1，3） D、（4，1）

查看试题解析
9. 如图，从边长为 $(a + 4) c m$ 的正方形纸片中剪去一个边长为 $(a + 1) c m$ 的正方形，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则拼成的矩形的面积是（　　） $c m^{2}$ .

A、 $(2 a^{2} + 5 a)$ B、 $3 a + 15$ C、 $(6 a + 9)$ D、 $(6 a + 15)$

查看试题解析
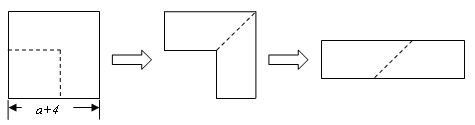10. 下列分解因式正确的是（　　）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $m^{2} + m - 6 = (m + 3) (m - 2)$ C、 $(a + 4) (a - 4) = a^{2} - 16$ D、 $x^{2} + y^{2} = (x - y) (x + y)$

查看试题解析

二、填空题（18分）

11. ${(- \frac{2}{3})}^{2012} \times {(\frac{3}{2})}^{2013} =$ ．

查看试题解析
12. 将2x²﹣8分解因式的结果是．

查看试题解析
13. .如图所示，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A'重合，若 $∠ A = 70 °$ ，则 $∠ 1 + ∠ 2 =$ .

查看试题解析
14. 如果P为整数，且 $(x + 4) (x + p) = x^{2} + m x - 12$ ，则m的值为．

查看试题解析
15. 如图，等腰三角形ABC的底边BC长为5，面积是20，腰AC的垂直平分线EF分别交AC ， AB边于E ， F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为．

查看试题解析
16. 如图，已知四边形ABCD中， $A B = 10$ 厘米， $B C = 8$ 厘米， $C D = 12$ 厘米， $∠ B = ∠ C$ ，点E为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为时，能够使△BPE与△CQP全等．

查看试题解析

三、解答题

17. 因式分解：

(1)、 $x^{2} y ﹣ 4 y$ ；

(2)、 ${(m + n)}^{2} ﹣ 4 n (m + n) + 4 n^{2}$ ．

查看试题解析
18. 教科书中这样写道：“形如 $a^{2} \pm 2 a b + b^{2}$ 的式子称为完全平方式“，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值、最小值等问题．
例如：分解因式： $x^{2} + 2 x ﹣ 3$ ．
解：原式 $= (x^{2} + 2 x + l) ﹣ 4 = {(x + 1)}^{2} ﹣ 4 = (x + 1 + 2) (x + 1 ﹣ 2) = (x + 3) (x ﹣ 1)$
再如：求代数式 $2 x^{2} + 4 x ﹣ 6$ 的最小值．
解： $2 x^{2} + 4 x ﹣ 6 = 2 (x^{2} + 2 x ﹣ 3) = 2 {(x + 1)}^{2} ﹣ 8$ ，可知当 $x = ﹣ 1$ 时， $2 x^{2} + 4 x ﹣ 6$ 有最小值，最小值是－8．
根据阅读材料，用配方法解决下列问题：

(1)、分解因式： $x^{2} ﹣ 6 x ﹣ 7 =$ ．（直接写出结果）

(2)、当x为何值时，多项式 $﹣ 2 x^{2} ﹣ 4 x + 5$ 有最大值？并求出这个最大值．

(3)、利用配方法，尝试求出等式 $a^{2} + 5 b^{2} ﹣ 4 a b ﹣ 2 b + 1 = 0$ 中a ， b的值．

查看试题解析
19. 图1、图2、图3都是3×3的正方形网格，每个小正方形的顶点称为格点，A、B、C均为格点．在给定的网格中，按下列要求画图：

(1)、在图1中，画一条不与AB重合的线段MN ，使MN与AB关于某条直线对称，且M、N为格点；

(2)、在图2中，画一条不与AC重合的线段PQ ，使PQ与AC关于某条直线对称，且P、Q为格点；

(3)、在图3中，画一个△DEF ，使△DEF与△ABC关于某条直线对称，且D．E、F为格点，符合条件的三角形共有个．

查看试题解析
20.

(1)、如图①，△ABC中，点D ， E在边BC上，AD平分∠BAC ， AE⊥BC ， $∠ B = 35 °$ ， $∠ C = 65 °$ ，求∠DAE的度数；

(2)、如图②，若把（1）中的条件“AE⊥BC”变成“F为DA延长线上一点，FE⊥BC”，其他条件不变，求∠F的度数．

查看试题解析
21. 如图，分别过点 $C$ 、 $B$ 作 $△ A B C$ 的 $B C$ 边上的中线 $A D$ 及其延长线的垂线，垂足分别为 $E$ 、 $F$ .

(1)、求证： $B F = C E$ ；

(2)、若 $△ A C E$ 的面积为4， $△ C E D$ 的面积为3，求△ABF的面积.

查看试题解析
22. 如图，点P是∠AOB外的一点，点Q与P关于OA对称，点R与P关于OB对称，直线QR分别交OA、OB于点M、N，若PM＝PN＝4，MN＝5．

(1)、求线段QM、QN的长；

(2)、求线段QR的长．

查看试题解析
23. 如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法，解答下列问题：

(1)、如图②，在△ABC中，∠ACB是直角， $∠ B = 60 °$ ， AD．CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系；

(2)、如图③，在△ABC中，如果∠ACB不是直角，而（1）中的其它条件不变，请问，你在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

查看试题解析
24. 如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．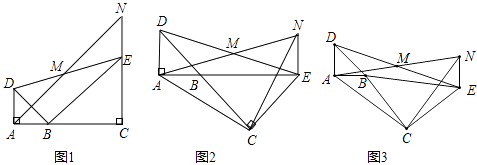

(1)、当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

(2)、将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；

(3)、将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

查看试题解析