广东省茂名市高州市十二校联考2023-2024学年八年级上学期(15周)月考数学试题
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 下列各组数中,是勾股数的是( )A、1,2,3 B、5,12,13 C、0.3,0.4,0.5 D、4,6,82. 49的平方根是( )
A、 B、7 C、 D、不存在3. 点关于轴对称的点的坐标为( )A、 B、 C、 D、4. 下列各点在直线上的是( )A、 B、 C、 D、5. 下列函数中,y是x的一次函数的是( )A、 B、 C、 D、6. 下列计算,正确的是( )A、 B、 C、 D、7. 下列函数图象中,表示直线的是( )A、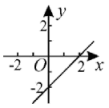 B、
B、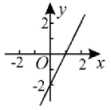 C、
C、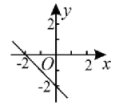 D、
D、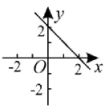 8. 已知是方程的一个解,那么的值是( )A、3 B、2 C、1 D、09. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为黑棋(乙)的坐标为 , 则白棋(甲)的坐标是( )
8. 已知是方程的一个解,那么的值是( )A、3 B、2 C、1 D、09. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为黑棋(乙)的坐标为 , 则白棋(甲)的坐标是( )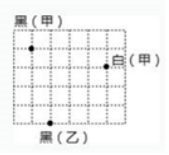 A、 B、 C、 D、10. 如图,在中,于 , 则的长是( )
A、 B、 C、 D、10. 如图,在中,于 , 则的长是( )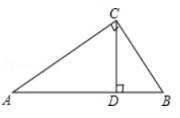 A、10 B、 C、 D、
A、10 B、 C、 D、二、填空题(本大题共5小题,每题3分,共15分.)
-
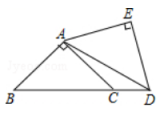
11. 计算: 的值是 .12. 若 , 则 .13. 已知点到轴的距离为3,到轴距离为2,且在第四象限内,则点的坐标为 .14. 在一次函数图象上有和两点,且 , 则(填“>,<或=”).15. 把两个同样大小的含角的三角尺按如上图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 , 且另三个锐角顶点在同一直线上,若 , 则 .
三、解答题(一)(本大题3小题,每小题6分,共18分)
-
16. 化简:17. 解方程组:18. 如图,实数在数轴上对应点的位置如图所示,化简的结果.
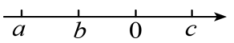
四、解答题(二)(本大题3小题,每小题7分,共21分)
-
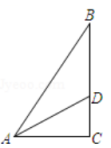
19. 如图,已知中,为的角平分线, , 求的长.
 20. 在平面直角坐标系中,已知点 .(1)、若点在轴上,求点的坐标;(2)、若点在第二、四象限的角平分线上,求点的坐标.21. 已知点和点关于轴对称,求的值.
20. 在平面直角坐标系中,已知点 .(1)、若点在轴上,求点的坐标;(2)、若点在第二、四象限的角平分线上,求点的坐标.21. 已知点和点关于轴对称,求的值.五、解答题(三)(本大题2小题,每小题8分,共16分)
-
22. 如图,在平面直角坐标系中,各顶点都在小方格的格点上.
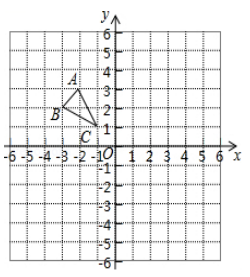 (1)、画出关于轴对称的 , 并写出各顶点的坐标;(2)、在轴上找一点 , 使得最短,画出图形,直接写出的最小值,并求出点坐标.23. 综合与实践
(1)、画出关于轴对称的 , 并写出各顶点的坐标;(2)、在轴上找一点 , 使得最短,画出图形,直接写出的最小值,并求出点坐标.23. 综合与实践【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯 , 如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离 .
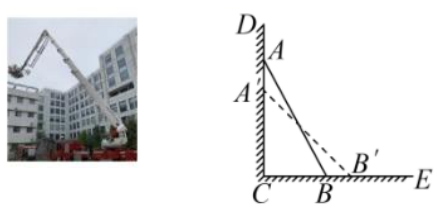 (1)、【深入探究】消防员接到命令,按要求将云梯从顶端A下滑到位置上(云梯长度不改变), , 那么它的底部B在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.(2)、【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的 , 则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
(1)、【深入探究】消防员接到命令,按要求将云梯从顶端A下滑到位置上(云梯长度不改变), , 那么它的底部B在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.(2)、【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的 , 则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?六、解答题(四)(本大题2小题,每小题10分,共20分)
-
24. 直线分别与轴交于两点,过点的直线交轴轴负半轴于 , 且 .
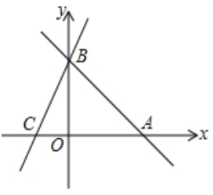 (1)、求点的坐标为;(2)、求直线的解析式;(3)、动点从出发沿射线方向运动,运动的速度为每秒1个单位长度.设运动秒时,当为何值时为等腰三角形.25. 定义:我们把一次函数与正比例函数的交点称为一次函数的“不动点”.例如求的“不动点”;联立方程 , 解得 , 则的“不动点”为 .(1)、由定义可知,求一次函数的“不动点”.(2)、若一次函数的“不动点”为 , 求的值.(3)、若直线与x轴交于点 , 与轴交于点 , 且直线上没有“不动点”,若点为轴上一个动点,使得 , 求满足条件的点坐标.
(1)、求点的坐标为;(2)、求直线的解析式;(3)、动点从出发沿射线方向运动,运动的速度为每秒1个单位长度.设运动秒时,当为何值时为等腰三角形.25. 定义:我们把一次函数与正比例函数的交点称为一次函数的“不动点”.例如求的“不动点”;联立方程 , 解得 , 则的“不动点”为 .(1)、由定义可知,求一次函数的“不动点”.(2)、若一次函数的“不动点”为 , 求的值.(3)、若直线与x轴交于点 , 与轴交于点 , 且直线上没有“不动点”,若点为轴上一个动点,使得 , 求满足条件的点坐标.