湖北省孝感市汉川市2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2024-02-02 类型：期中考试
一、精心选一选，相信自己的判断!（本大题共8小题，每小题3分，共24分.在每小题给
-
1. 某校为庆祝2023年9月23日至10月8日在杭州举行的第19届亚运会，特举办了以《中国加油》为主题的手抄报活动，以下汉字是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知一个三角形三边长分别为3，x，6，则x的值可能是（ ）A、14 B、12 C、10 D、83. 在平面直角坐标系中，点A（m，2）与点B（3，n）关于x轴对称，则m，n的值是（ ）A、m＝﹣3，n＝2 B、m＝2，n＝3 C、m＝3，n＝﹣2 D、m＝﹣2，n＝34. 如图，已知∠BAC＝∠DAC，添加一个条件仍不能判定△ABC≌△ADC的是（ ）
A、AB＝AD B、BC＝CD C、∠BCE＝∠DCE D、∠B＝∠D5. 过n边形的一个顶点可以作2023条对角线，则这个n边形的边数是（ ）A、2023 B、2024 C、2025 D、20266. 如图所示，是用直尺和圆规作一个角等于已知角的示意图，则说明∠A′O′B′＝∠AOB的依据是（ ）
A、SAS B、SSS C、AAS D、ASA7. 如图，在△ABC中，∠BAC＝130°，AB的垂直平分线交AB于点D，交BC于点E，AC的垂直平分线交AC于点G，交BC于点F，连接AE，AF，则∠EAF的度数为（ ）
A、65° B、80° C、100° D、110°8. 如图，点D在△ABC内部，且DA＝DB＝DC，点E在AB边上，且EB＝EC，∠AEC＝60°，连接ED并延长交BD于点F．以下结论：①EF⊥BC；②∠BAD+∠BCD＝30°；③∠ADC＝60°；④AE+DE＝BE．其中正确的结论有（ ）
A、4个 B、3个 C、2个 D、1个二、细心填一填，试试自己的身手!（本大题共8小题，每小题3分，共24分)
-
9. 盖房子时，在窗框未安装好之前，木工师傅常常先在窗框上斜钉一根木条固定门框，使其不变形，如图所示，这是利用了三角形的性．
10. 一个等腰三角形的两边长分别为4cm和8cm，则周长是 cm．11. 一个n边形的每个内角都等于144°，则n＝ ．12. 如图，AC＝AD，∠BAE＝∠CAD，要使△ABC≌△AED，应添加的条件是 ． （写出一个正确条件即可）
13. 如图，△ABC的角平分线相交于点O，已知AB＝4，AC＝8，BC＝10，则S△ABO：S△ACO：S△BCO＝ ．
14. 如图，四边形ABCD是轴对称图形，BD所在的直线是它的对称轴，AB＝3.1cm，CD＝2.3cm．则四边形ABCD的周长为 ．
15. 如图，∠ACD是△ABC的外角，∠ABC与∠ACD的平分线交于点A1 ， ∠A1BC与∠A1CD的平分线交于点A2 ， ∠A2BC与∠A2CD的平分线交于点A3 ， …，∠A2023BC与∠A2023CD的平分线交于点A2024 ， 若∠A＝α，则∠A2024的度数为°．（用含α的式子表示）
16. 如图，△ABC和△DEF是两个等腰直角三角形，∠BAC＝∠DFE＝90°，AB＝AC，FD＝FE，△DEF的顶点E在边BC上移动，在移动过程中，线段DE与线段AB相交于点P，线段EF与线段CA相交于点Q，连接AE、PQ．当E为BC中点时，若AP＝9，AQ＝12，PQ＝15，则AC的长为 ．
三、用心做一做（本大题共8小题，满分72分.请认真读题，冷静思考.解答题应写出必要
-
17. 分别求出下列图形中x和y的值．
18. 我们把两组邻边相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD．对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E，F．求证OE=OF．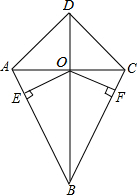
19. 如图，△ABC中，∠B＝90°，DE⊥AC于点E，点F在AB上，且CE＝FB，CD＝FD．
(1)、求证：AD平分∠BAC；(2)、∠AFD与∠C的数量关系是 ．20. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣4，2），B（﹣2，4），C（﹣1，1）．
(1)、画出△ABC关于x轴对称的△A1B1C1 ， 并写出点A1 ， B1 ， C1的坐标；(2)、已知点D在y轴的正半轴上，且∠CDA＝45°，点D的坐标为 ．21. 如图，在等腰△ABC中，AB＝AC，点D，E，F在△ABC的边上，满足BE＝CF，BD＝CE．
(1)、求证：DE＝EF；(2)、已知∠A＝70°，求∠DEF的度数．22. 在△ABC中，AC＝BC，∠ACB＝90°，AE平分∠BAC交BC于点E，BD⊥AE交AE延长线于点D，连接CD，过点C作CF⊥CD交AD于F．
(1)、如图1，①求∠EBD的度数；②求证：AF＝BD；(2)、如图2，DM⊥AC交AC的延长线于点M，请直接写出AB，AC，AM之间的数量关系为 ．23. △ABC中，∠ABC和∠ACB的平分线BD，CE相交于点O，记∠BAC＝x，∠BOC＝y．
(1)、如图1．①若x＝50°，则y＝ ▲ ；
②请你根据①中计算的心得猜想写出y与x的关系式，并证明你猜想的正确性；
(2)、如图2，启智学校内有一个三角形的小花园，花园中有两条小路BD和CE为△ABC的角平分线，交点为点O，在O处建有一个自动浇水器，需要在BC边上取一处接水口F，经过测量得知∠BAC＝120°，OD⋅OE＝12000m2 ， BC﹣BE﹣CD＝160m，请你求出水管OF至少要多长？24. 如图
(1)、【积累经验】萌萌学完全等三角形的知识后，遇到了这样一个问题：如图1，DA⊥AB于点A，CB⊥AB于点B，点E在线段AB上，连接DE，CE，∠DEC＝90°，且DE＝CE．求证：AD＝BE，AE＝BC．萌萌发现只需证明△≌△即可；
(2)、【类比应用】如图2，在平面直角坐标系中，在△ABC中，∠ACB＝90°，AC＝BC，已知点A的坐标为（0，3），点C的坐标为（2，0），求点B的坐标；
(3)、【拓展提升】如图3，在平面直角坐标系中，点A的坐标为（﹣6，0），点B为y轴正半轴上一动点，分别以OB，AB为边在第一，第二象限中分别作等腰直角△OBF，等腰直角△ABE，∠ABE＝∠OBF＝90°，连接EF交y轴于点P，当点B在y轴上移动时，PB的长度是否发生改变？若不变，求出PB的值；若变化，求PB的取值范围．