广东省惠州市大亚湾六校联考2023-2024学年九年级上册第三次月考数学试题

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 下列国产新能源汽车标志，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 平面内，已知 $⊙ O$ 的半径为 $10 c m ， P O = 12 c m$ ，则点 $P$ 与 $⊙ O$ 的位置关系是（）

A、点 $P$ 在 $⊙ O$ 上 B、点 $P$ 在 $⊙ O$ 内 C、点 $P$ 在 $⊙ O$ 外 D、不能确定

查看试题解析
3. 用配方法解一元二次方程 $x^{2} + 4 x = 5$ 时，此方程可变形为（）

A、 ${(x + 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 用反证法证明“ $△ A B C$ 中至少有两个锐角”，第一步应为（）

A、假设 $△ A B C$ 中至多有一个锐角 B、假设 $△ A B C$ 中有一个直角 C、假设 $△ A B C$ 中有两个直角 D、假设 $△ A B C$ 中有两个锐角

查看试题解析
5. 下列关于抛物线 $y = (x - 1)^{2} + 3$ 的说法不正确的是（）

A、抛物线开口向上 B、抛物线的顶点是（1，3） C、抛物线与y轴的交点是（0，3） D、当x>1时，y随x的增大而增大

查看试题解析
6. 关于x的一元二次方程 $x^{2} - 5 x + m = 0$ 有两个不相等的实数根，则实数m的取值范围是（）

A、 $m < \frac{25}{4}$ B、 $m \leq \frac{25}{4}$ C、 $m > \frac{25}{4}$ D、 $m \geq \frac{25}{4}$

查看试题解析
7. 如图，将 $△ A B C$ 绕点C旋转得到 $△ D E C$ ，点A对应点D ，点B对应点E ，点B刚好落在 $D E$ 边上， $∠ A = 24 ° ， ∠ B C D = 48 °$ ，则 $∠ A B C =$ （）

A、 $68 °$ B、 $70 °$ C、 $72 °$ D、 $74 °$

查看试题解析
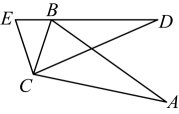8. 如图，点A、B、C、D为一个正多边形的顶点，点O为正多边形的中心，若 $∠ A D B = 18 °$ ，则这个正多边形的边数为（）

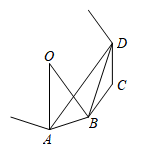A、10 B、12 C、15 D、20

查看试题解析
9. 筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图1，点M表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O为圆心，5m为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB长为8m，则筒车工作时，盛水桶在水面以下的最大深度为（）

A、1米 B、2米 C、3米 D、4米

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 中两个变量的x与y的3组对应值：点 $P (x_{1} ， y_{1}) ， Q (x_{2} ， y_{2})$ 在该函数图象上．若当 $x_{1} < x_{2} < 3$ 时， $- 1 < y_{1} < y_{2}$ ，给出下列3个结论：① $a < 0$ ；② $x_{1} + x_{2} < 4$ ；③ $25 a - 5 b + c + 1 < 0$ ．上述结论中，所有正确结论的序号是（）
x
……
$- 3$
3
7
……
y
……
m
$- 1$
m
……

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 如图，圆锥的母线长 $l$ 为 $10 c m$ ，底面圆半径 $r$ 为 $4.5 c m$ ，则该圆锥的侧面积为 $c m^{2}$ ．

查看试题解析
12. 根据物理学规律，如果不考虑空气阻力，以 $40 m / s$ 的速度将小球沿与地面成 $30 °$ 角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是： $h = - 5 t^{2} + 20 t$ ，则小球运动中的最大高度是m．

查看试题解析
13. 如图，将边长为为3厘米的正方形 $A B C D$ 绕点C按顺时针方向旋转 $30 °$ ，得到正方形 $E F C G$ ， $E F$ 与 $A D$ 交于H ，则 $D H$ 的长是厘米．

查看试题解析
14. 关于x的一元二次方程 $x^{2} + x = n$ 有两个不相等的实数根，则抛物线 $y = x^{2} + x - n$ 的顶点在第象限．

查看试题解析
15. 在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果.如图，利用黄金分割法，所做 $E F$ 将矩形窗框 $A B C D$ 分为上下两部分，其中E为边 $A B$ 的黄金分割点，即 $B E^{2} = A E \cdot A B$ .已知 $A B$ 为2米，则线段 $B E$ 的长为米.

查看试题解析

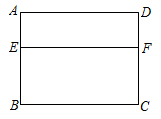
三、解答题（一）（本大题共3小题，16题10分，第17，18题各7分，共24分）

16.

(1)、解方程： $x (2 x - 5) = 2 x - 5$

(2)、已知关于x的一元二次方程 $x^{2} - 4 x - 2 m + 5 = 0$ 的一个根为3，求实数m的值及另一个根．

查看试题解析
17. 如图，利用一面墙（墙的长度不限），另三边用20米长的篱笆围成一个矩形场地．若围成矩形场地的面积为50米² ，求矩形场地的长和宽．

查看试题解析
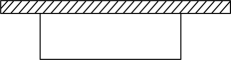18. 综合与实践
将两个全等的的 $R t △ A B C$ 和 $R t △ D E C$ ，其中 $∠ A B C = ∠ D E C = 90 °$ ，按如图1方式放置， $A B$ 与 $D E$ 交于点O ．

(1)、通过观察和测量，猜想 $A E 、 B D$ 的数量关系为； $C O$ 与 $A D$ 的位置关系是；

(2)、将 $R t △ D E C$ 绕点C逆时针旋转至图2所示的位置，（1）中的猜想是否还成立，若成立，请证明；不成立，请说明理由．

查看试题解析

四、解答题（二）（本大题共3小题，每小题9分，共27分）

19. 如图，已知抛物线 $y_{1} = x^{2} - 3 x + 2$ 与直线 $A B$ ： $y_{2} = k x + m (k \neq 0)$ 交于 $A (1 ， 0) ， B (0 ， 2)$ 两点，顶点为D ．

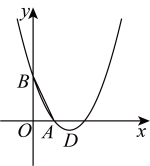(1)、请根据图象直接写出 $y_{1} > y_{2}$ 时x的取值范围；

(2)、将 $△ O A B$ 绕点A顺时针旋转 $90 °$ 后，点B落到点C的位置，将抛物线沿y轴平移后经过点C ，求平移后所得抛物线的解析式．

查看试题解析
20. 如图所示，它是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点……，第 $n$ 行有 $n$ 个点，……

(1)、第一行有1个点，前两行点数和是3，前三行点数和是6，请问前四行的点数和是，前 $n$ 行的点数和是；

(2)、探究发现，120是前行的点数和；

(3)、三角点阵中前 $n$ 行的点数和能是600吗？如果能请求出；如果不能，试用一元二次方程说明理由．

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B A C$ 的角平分线 $A D$ 交 $B C$ 边于点D ．

(1)、以 $A B$ 边上一点O为圆心，过A ， D两点作 $⊙ O$ （不写作法，保留作图痕迹）；

(2)、判断直线 $B C$ 与 $⊙ O$ 的位置关系，并说明理由；

(3)、若（1）中的 $⊙ O$ 与边AB的另一个交点为E ， $A B = 6$ ， $B D = 2 \sqrt{3}$ ，求 $\overset{⌢}{D E}$ 的弧长（结果保留根号和π）．

查看试题解析

五、解答题（三）（本大题共2小题，每小题12分，共24分）

22. 综合探究
（一）新知学习：
人教版数学九年级上教材第119页《探究四点共圆的条件》发现，圆内接四边形的判断定理：如果四边形对角互补，那么这个四边新内接于圆（即如果四边形EFGH的对角互补，那么四边形 $E F G H$ 的四个顶点E、F、G、H都在同个圆上）．
（二）问题解决：
已知 $⊙ O$ 的半径为2， $A B ， C D$ 是 $⊙ O$ 的直径，P是 $\overset{⌢}{B C}$ 上任意一点，过点P分别作 $A B ， C D$ 的垂线，垂足分别为N ， M ．

(1)、若直径 $A B ⊥ C D$ （如图1），在点P（不与B、C重合）从B运动到C的过程中， $M N$ 的长是否为定值，若是，请并求出其定值；若不是，请说明理由．

(2)、若直径 $A B$ 与 $C D$ 相交成 $120 °$ 角，当点P（不与B、C重合）从B点运动到C的过程中（如图2），证明 $M N$ 的长为定值．

(3)、试问当直径 $A B$ 与 $C D$ 相交成多少度角时， $M N$ 的长取最大值，并写出其最大值．

查看试题解析
23. 综合运用
如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 与 $x$ 轴交于 $A (3 ， 0)$ 、 $B (- 1 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ，连接 $A C$ ．

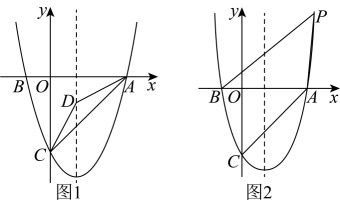(1)、求抛物线的解析式与顶点 $M$ 坐标；

(2)、如图1，在对称轴上是否存在一点 $D$ ，使 $∠ D C A = ∠ D A C$ ，若存在，请求出点 $D$ 的坐标；若不存在，请说明理由；

(3)、如图2，若点 $P$ 是抛物线上的一个动点，且 $∠ A P B = 45 °$ ，请直接写出点 $P$ 的横坐标．

查看试题解析

x	……	$- 3$	3	7	……
y	……	m	$- 1$	m	……