浙江省杭州市滨江区重点学校2023-2024学年九年级上学期开学数学试卷
试卷更新日期:2024-02-02 类型:开学考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 要使二次根式有意义,则的值可以为( )A、 B、 C、 D、2. 把一元二次方程化成一般形式,正确的是( )A、 B、 C、 D、3. 反比例函数y= (x<0)的图象位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 将抛物线y=-5x +1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( ).
A、y=-5(x+1)2 -1 B、y=-5(x-1)2 -1 C、y=-5(x+1)2 +3 D、y=-5(x-1)2 +35. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<26. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、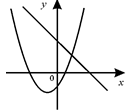 B、
B、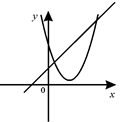 C、
C、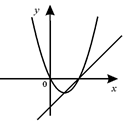 D、
D、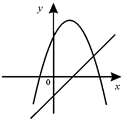 7. 如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:这个四边形可能是正方形这个四边形一定是菱形这个四边形不可能是矩形这个四边形一定是轴对称图形,其中正确的论断是( )
7. 如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:这个四边形可能是正方形这个四边形一定是菱形这个四边形不可能是矩形这个四边形一定是轴对称图形,其中正确的论断是( )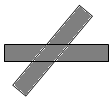 A、 B、 C、 D、8. 某农场拟建两间矩形饲养室,一面靠现有墙墙足够长 , 中间用一道墙隔开,并在如图所示的三处各留宽的门,已知计划中的材料可建墙体不包括门总长为 , 则能建成的饲养室的总面积最大为( )
A、 B、 C、 D、8. 某农场拟建两间矩形饲养室,一面靠现有墙墙足够长 , 中间用一道墙隔开,并在如图所示的三处各留宽的门,已知计划中的材料可建墙体不包括门总长为 , 则能建成的饲养室的总面积最大为( )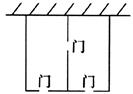 A、 B、 C、 D、9. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
A、 B、 C、 D、9. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )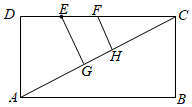 A、 B、 C、3 D、10. 已知二次函数为非零常数, , 当时,随的增大而增大,则下列结论正确的是( )
A、 B、 C、3 D、10. 已知二次函数为非零常数, , 当时,随的增大而增大,则下列结论正确的是( )若时,则随的增大而减小;若图象经过点 , 则;若 , 是函数图象上的两点,则;若图象上两点 , 对一切正数总有 , 则 .
A、 B、 C、 D、二、填空题:本题共6小题,每小题4分,共24分。
-
11. 若是方程的一个根,则代数式的值为 .12. 在二次函数中,函数与自变量的部分对应值如下表:
则、的大小关系为填“”,“”或“”
13. 已知抛物线与关于原点成中心对称,若抛物线的解析式为 , 则抛物线的解析式为 .14. 已知函数的图象与坐标轴只有两个交点,则 .15. 如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点 , 反比例函数的图象恰好经过点 , 若直尺的宽 , 三角板的斜边 , 则 . 16. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为 , 是它的较短对角线,点、分别是边 , 上的两个动点,且满足 , 设的面积为 , 则的取值范围是 .
16. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为 , 是它的较短对角线,点、分别是边 , 上的两个动点,且满足 , 设的面积为 , 则的取值范围是 .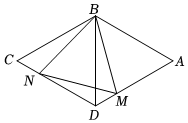
三、计算题:本大题共1小题,共10分。
-
17. 如图,在▱ 中,点 , 分别是 , 的中点,点 , 在对角线 上,且 .
 (1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.
(1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.四、解答题:本题共6小题,共56分。解答应写出文字说明,证明过程或演算步骤。
-
18. 计算与解方程:(1)、;(2)、19. 如图,一次函数的图象分别与轴,轴交于 , 两点,将点先向右平移2个单位,再向上平移5个单位后,得到的点恰好落在反比例函数的图象上.
 (1)、求该反比例函数的表达式;(2)、已知点是该反比例函数图象上一点,当时,请根据图象直接写出横坐标的取值范围.20. 已知二次函数 .
(1)、求该反比例函数的表达式;(2)、已知点是该反比例函数图象上一点,当时,请根据图象直接写出横坐标的取值范围.20. 已知二次函数 .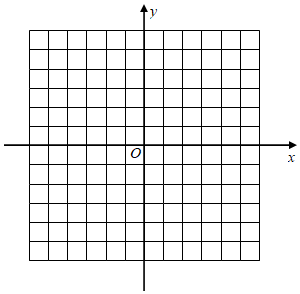 (1)、求出该函数图象的顶点坐标,对称轴,图象与轴、轴的交点坐标,并在所给的坐标系中画出这个函数的大致图象.(2)、利用函数图象直接写出:
(1)、求出该函数图象的顶点坐标,对称轴,图象与轴、轴的交点坐标,并在所给的坐标系中画出这个函数的大致图象.(2)、利用函数图象直接写出:当时,的取值范围?
当时,的取值范围?
21. 篮球运动员投篮后,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为直线x=2.5.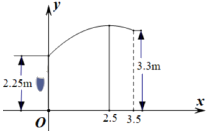 (1)、求篮球运动路线的抛物线表达式和篮球在运动中离地面的最大高度.(2)、若篮筐离地面3.05m , 离运动员投篮处水平距离为4.2m , 问:篮球以该运动方式,能否投进篮筐?若能投进篮筐,请说明理由;若不能,则运动员应向前还是往后移动多少米后再投篮,刚好能使篮球投进篮筐?
(1)、求篮球运动路线的抛物线表达式和篮球在运动中离地面的最大高度.(2)、若篮筐离地面3.05m , 离运动员投篮处水平距离为4.2m , 问:篮球以该运动方式,能否投进篮筐?若能投进篮筐,请说明理由;若不能,则运动员应向前还是往后移动多少米后再投篮,刚好能使篮球投进篮筐?
-
