浙江省杭州市萧山区八校联考2023-2024学年八年级上学期12月份数学试题
试卷更新日期:2024-02-02 类型:月考试卷
一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.
-
1. 2023年第19届亚运会是一场规模盛大的体育盛事,下列体育图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在数轴上表示不等式﹣1≤x<3,正确的是( )A、
2. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在数轴上表示不等式﹣1≤x<3,正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 等腰三角形的两边长分别为8和14,则这个三角形的周长为( )A、22 B、30或22 C、36 D、30或365. 如图,将两根等长钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工件,则的长等于容器内径 , 那么判的理由是( )
4. 等腰三角形的两边长分别为8和14,则这个三角形的周长为( )A、22 B、30或22 C、36 D、30或365. 如图,将两根等长钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工件,则的长等于容器内径 , 那么判的理由是( ) A、边边边 B、边角边 C、角边角 D、角角边6. 甲、乙两地相距 , 一货车从甲地出发以的速度匀速向乙地行驶,则货车距离乙地的路程与时间之间的函数表达式是( )A、 B、 C、 D、7. 对于命题“如果 ,那么 .”能说明它是假命题的反例是( )A、 B、 , C、 , D、 ,8. 如图,的面积为 , 垂直于的平分线于 , 则的面积( )
A、边边边 B、边角边 C、角边角 D、角角边6. 甲、乙两地相距 , 一货车从甲地出发以的速度匀速向乙地行驶,则货车距离乙地的路程与时间之间的函数表达式是( )A、 B、 C、 D、7. 对于命题“如果 ,那么 .”能说明它是假命题的反例是( )A、 B、 , C、 , D、 ,8. 如图,的面积为 , 垂直于的平分线于 , 则的面积( )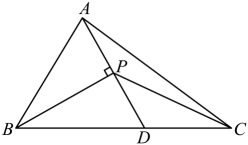 A、 B、 C、 D、9. 如图,在中,和的平分线 , 相交于点O,交于E,交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的个数是( )
A、 B、 C、 D、9. 如图,在中,和的平分线 , 相交于点O,交于E,交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的个数是( )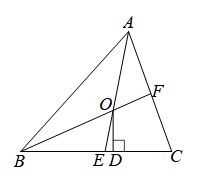 A、1个 B、2个 C、3个 D、0个10. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )
A、1个 B、2个 C、3个 D、0个10. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )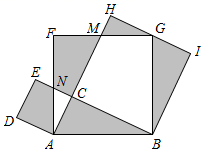 A、3 B、 C、2 D、
A、3 B、 C、2 D、二、认真填一填(本题有6个小题,每小题4分,共24分)
-
11. 已知一次函数 , 当自变量时,函数y的值是 .12. 若点在x轴上,点在y轴上,则代数式的值是 .13. 小明同学将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件是 .
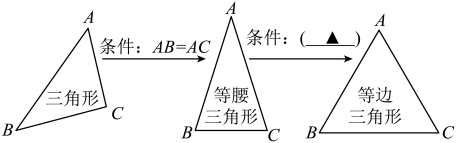 14. 不等式组的解集是 , 则a的取值范围是 .15. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形两边的长, 且这个等腰三角形的周长为7,则 的值为 .16. 如图,A,B,C,D四个点顺次在直线l上, , . 以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且 . 当时,和的面积和是 . 连结 , , 当的长度变化时,与的面积之差保持不变,则a与b需满足的条件是 .
14. 不等式组的解集是 , 则a的取值范围是 .15. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形两边的长, 且这个等腰三角形的周长为7,则 的值为 .16. 如图,A,B,C,D四个点顺次在直线l上, , . 以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且 . 当时,和的面积和是 . 连结 , , 当的长度变化时,与的面积之差保持不变,则a与b需满足的条件是 .
三、全面答一答(本题有8个小题,共66分)
-
17. 解不等式(组)(1)、4x≤3x+7(2)、18. 如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题:
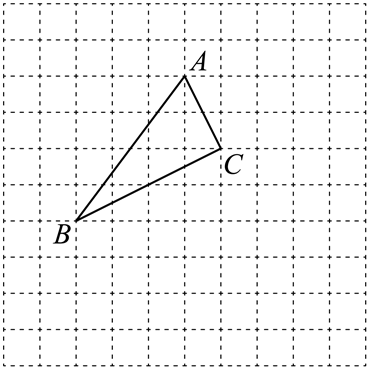 (1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出B和C的坐标;(3)、在图中画出△ABC关于x轴对称的△A1B1C1 .19. 如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
(1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出B和C的坐标;(3)、在图中画出△ABC关于x轴对称的△A1B1C1 .19. 如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.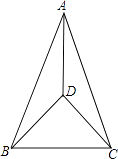 20. 已知y是x的一次函数,且当时,;当时, .(1)、求此函数表达式和自变量x的取值范围.(2)、当时,求自变量x的取值范围.(3)、若 , , 对应的函数值分别为 , . 比较与的大小.21. 如图,是等边三角形,D是边AB上一点,以CD为边作E等边 , DE交AC于点F,连接AE,
20. 已知y是x的一次函数,且当时,;当时, .(1)、求此函数表达式和自变量x的取值范围.(2)、当时,求自变量x的取值范围.(3)、若 , , 对应的函数值分别为 , . 比较与的大小.21. 如图,是等边三角形,D是边AB上一点,以CD为边作E等边 , DE交AC于点F,连接AE,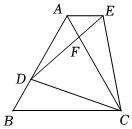 (1)、求证:≌(2)、若 , , 求CD的长.22. 已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)、求证:≌(2)、若 , , 求CD的长.22. 已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.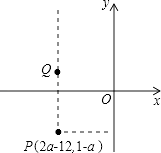 (1)、若点P的纵坐标为﹣3,试求出a的值;
(1)、若点P的纵坐标为﹣3,试求出a的值;
(2)、在(1)题的条件下,试求出符合条件的一个点Q的坐标;(3)、若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.23. 为建设美丽郑州,某治污公司决定购买10台污水处理设备.现有 , 两种型号的设备,其中每台的价格与月处理污水量如下表:型
型
价格(万元/台)
处理污水量(吨/月)
240
200
经调查:购买一台型设备比购买一台型设备多2万元,购买2台型设备比购买3台型设备少6万元.
(1)、求 , 的值;(2)、如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;(3)、在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.24. 如图 (1)、【证明体验】
(1)、【证明体验】如图1,在中,为边上的中线,延长至 , 使 , 连接 . 求证: .
(2)、【迁移应用】如图2,在中, , , 为的中点, . 求面积.
(3)、【拓展延伸】如图3,在中, , 是延长线上一点, , 是上一点,连接交于点 , 若 , , 求的长.