北师大版六年级数学下册第一单元测试B卷
试卷更新日期：2024-02-02 类型：单元试卷
一、填空题。 (14 分)
-
1. 点动成 ， 例如：一颗流星划过夜空；线动成 ， 例如：秒针在钟面上旋转一周形成圆；面动成 ， 例如：同学们小时候玩过的拉花，旋转一周后形成球形的灯笼。2. 圆柱的底面积是 ， 侧面积是 ， 这个圆柱的表面积是3. 将一个圆柱形易拉罐(如下图)展开，得到一个长 12.56 cm，宽8 cm的长方形及两个大小相同的圆。这个易拉罐的侧面积是它的一个底面的面积是cm²，表面积是
4. 一个圆柱的底面半径是 2d m，高是2d m，它的体积是。5. 两个底面积相等的圆柱，一个圆柱的高为4d m，体积为 ， 另一个圆柱的高为8dm，体积为dm³。6. 一个圆锥和一个圆柱，它们的底面积和高都相等，已知它们的体积之和是 ， 则圆锥的体积是。7. 用一张边长是18.84 cm的正方形围成一个尽可能大的圆柱，这个圆柱的底面积是 。8. 把一根长20cm的圆木锯成三段，每段仍是圆柱，表面积比原来增加了 ， 这根圆木原来的体积是cm³。9. 一台压路机前轮直径是 1.5m ，轮宽4m ，前轮滚动一周，压路的面积是m²。10. 下图是一块长方形铁皮，利用图中涂色部分刚好能做成一个油桶。这个油桶的容积是(铁皮厚度忽略不计)。(单位：dm)
二、判断题。(5分)
-
11. 求长方体、正方体、圆柱、圆锥的体积，都可以用“底面积×高”来计算。 （ ）12. 如果两个圆柱的侧面积相等，那么它们的底面周长也相等。（ ）13. 一个圆柱形橡皮泥可以做成三个和它等底等高的圆锥。（ ）14. 因为电线杆的上、下两个底面都是圆形的，所以电线杆是圆柱。（ ）15. 圆锥的底面半径扩大3倍，高缩小3 倍后，圆锥的体积不变。（ ）
三、选择题。(将正确答案的序号填在括号里)(10分)
-
16. 下图中，以直线为轴旋转，可以得到圆柱的是 ， 可以得到圆锥的是。
A.
B.
C.
17. 一个圆柱和一个圆锥的底面半径的比是1：3，高的比也是1：3，它们的体积之比是（ ）。A、1：9 B、1：3 C、9：118. 一个圆柱形输油管，内直径是2dm，油充满整个管内的流速是4分米/秒，每秒流过的油是（ ）cm³。A、62.8 B、2.512 C、1256019. 把一个大圆柱分成两个小圆柱后发生变化的是（ ）。A、圆柱的体积 B、圆柱的表面积 C、圆柱的底面积20. 长方体包装盒的长是20cm，宽是4.6cm，高是1 cm，圆柱形零件的底面直径是2cm，高是1cm。这个包装盒内最多能放（ ）个零件。A、20 B、23 C、29四、计算题。(8 分)
-
21. 计算下列图形的表面积。(单位：dm)
22. 计算下列图形的体积。 (单位：dm)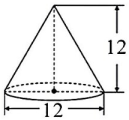
五、填表题。(16 分)
-
23.
名称
底面半径/cm
高/cm
侧面积/cm2
表面积/cm2
体积/cm3
圆柱
①
4
15
②
5
18.84
圆锥
③
5
1.2
④
1.5
2
六、仔细观察并作答。(10分)
-
24. 要制作一个无盖的圆柱形容器，有以下几种型号的铁皮可供选择。
(1)、你选择的材料是号和号。(2)、用你所选择的材料做成的圆柱形容器最多能装水多少千克? (1 L水约重1kg)七、解决问题。 (37 分)
-
25. 一个圆锥形的沙堆，占地面积是 ， 高是3.6m，如果每立方米的沙子重1.7t，这堆沙子共重多少吨?26. 砌一个圆柱形蓄水池，底面直径是1.2m，池深8 m，现在要把水池里面的四周和底面抹上一层水泥，抹水泥的面积是多少平方米? 这个水池大约能蓄水多少立方米?
-
-
