浙江省金华市义乌市五校2023-2024九年级上学期12月月考数学试题

试卷更新日期：2024-02-01 类型：月考试卷

进入出卷网下载

一、选择题

1. 成语“水中捞月”所描述的事件是（）.

A、必然事件 B、随机事件 C、不可能事件 D、无法确定

查看试题解析
2. ⊙O的半径为3，点O到直线l的距离为4，则反映直线l与⊙O位置关系的图形（）

A、 B、 C、 D、

查看试题解析
3. 如图，在△ABC中，若∠C＝90°，则（）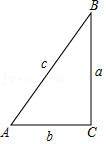

A、 $s i n A = \frac{a}{c}$ B、 $s i n A = \frac{b}{c}$ C、 $c o s A = \frac{a}{b}$ D、 $c o s A = \frac{b}{a}$

查看试题解析
4. 如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y＝﹣2x²﹣8x+m上的点，则（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₂＞y₁＞y₃ D、y₂＞y₃＞y₁

查看试题解析
6. 主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长20米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上（BP长为x），则x满足的方程是（）

A、（20﹣x）²＝20x B、x²＝20（20﹣x） C、x（20﹣x）＝20² D、以上都不对

查看试题解析
7. 如图，点C、D、E、F、G在以AB为直径的⊙O上，∠AGC＝20°，∠BFE＝10°，则∠CDE＝（）

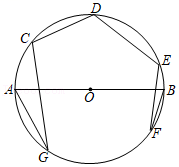A、115° B、120° C、135° D、150°

查看试题解析
8. 如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t² ，方程20t﹣5t²＝15的两根为t₁＝1与t₂＝3，下列对正确的是（）

A、小球的飞行高度为15m时，小球飞行的时间是1s B、小球飞行3s时飞行高度为15m，并将继续上升 C、小球从飞出到落地要用4s D、小球的飞行高度可以达到25m

查看试题解析
9. 如图，在矩形ABCD中，E是CD边的中点，且BE⊥AC于点F ，连接DF ，则下列结论错误的是（）

A、△ADC ∽△CFB B、 $\frac{B C}{A C} = \frac{1}{2}$ C、AD＝DF D、 $\frac{S_{Δ C E F}}{S_{Δ A B F}} = \frac{1}{4}$

查看试题解析
10. 如图，抛物线y＝﹣x²+2x+m+1交x轴于点A（a ， 0）和B（b ， 0），交y轴于点C ，抛物线的顶点为D ，下列四个命题：①当x＞0时，y＞0； ②若a＝﹣1，则b＝4；
③抛物线上有两点P（x₁ ， y₁）和Q（x₂ ， y₂），若x₁＜1＜x₂ ，且x₁+x₂＞2，则y₁＞y₂；
④点C关于抛物线对称轴的对称点为E ，点G ， F分别在x轴和y轴上，当m＝2时，四边形EDFG周长的最小值为 $6 \sqrt{2}$ ．其中真命题的序号是（）

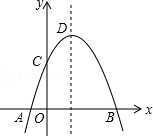A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 已知2x＝3y（y≠0），则 $\frac{x}{y} =$ ．

查看试题解析
12. 在函数y＝ $\frac{1}{2 x - 4}$ 中，自变量x的取值范围是．

查看试题解析
13. 已知弧长等于3π，弧所在圆的半径为6，则该弧的度数是．

查看试题解析
14. 如图，在直径为AB的⊙O中，点C ， D在圆上，AC＝CD ，若∠CAD＝28°，则∠DAB的度数为．

查看试题解析
15. 函数y＝x²﹣2ax﹣2在﹣1≤x≤2有最大值6，则实数a的值是．

查看试题解析
16. 如图，梯形OABC中，BC//AO，O(O，O)，A(10，0)，B(10，4)，BC=2，G(t，0)是底边OA上的动点，则tan∠OAC= ；边AB关于直线CG的对称线段为MN，若MN与△OAC的其中一边平行时，则t= 。

查看试题解析

三、解答题

17. 计算： $\sqrt{4}$ +2sin45°﹣（π﹣3）⁰+| $\sqrt{2}$ ﹣2|．

查看试题解析
18. 如图，在6×6的正方形网格中，每个小正方形的边长都为1，点A，B，C均在格点上．请按要求在网格中画图，所画图形的顶点均需在格点上．请在图2中画△DEF，在图3中画△PMN，使△DEF和△PMN不全等，且都与图1中的△ABC相似且不全等，并写出△DEF和△PMN的周长．
△DEF的周长＝ ▲ ；△PMN的周长＝ ▲

查看试题解析
19. 小汤对九年级学生参与“力学”、“热学”、“光学”、“电学”四个类别的物理实验情况进行了抽样调查，每位同学只能选其中一个类别，根据调查结果绘制了如图所示的不完整的频数分布表和扇形统计图（图1），请根据图表提供的信息，解答下列问题：
类别
频数（人数）
频率
力学
m
0.5
热学
8

光学
20
0.25
电学
12

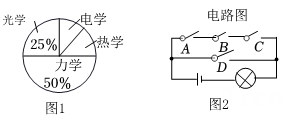(1)、m＝，热学对应的圆心角＝°．

(2)、如图，当小汤随机闭合A、B、C、D这4个开关中任意2个时，用树状图或列表法求出灯泡亮的概率．

查看试题解析
20. 如图，四边形ABCD内接于⊙O ， AC为⊙O的直径，∠ADB＝∠CDB ．

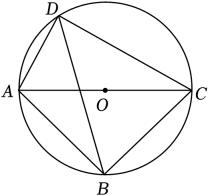(1)、试判断△ABC的形状，并给出证明；

(2)、若AB＝5 $\sqrt{2}$ ， AD＝6，求CD的长度．

查看试题解析
21. 为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装遮阳篷，便于社区居民休憩.
如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，当太阳光线AD与地面CE的夹角为45°时，求阴影CD的长.（结果精确到0.1米；参考数据： $s i n 16 ° ≈ 0.28$ ， $c o s 16 ° ≈ 0.96$ ， $t a n 16 ° ≈ 0.29$ ）

查看试题解析
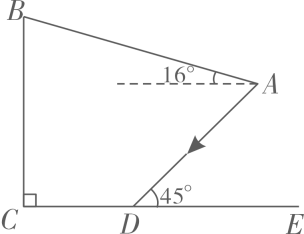22. 已知抛物线y＝x²﹣2mx+m²﹣1（m是常数）．

(1)、若抛物线y＝x²﹣2mx+m²﹣1的顶点在直线y＝2x上，求该抛物线的解析式；

(2)、若抛物线y＝x²﹣2mx+m²﹣1与x轴的两个交点分别为（x₁ ， 0），（x₂ ， 0）且 ${x_{1}}^{2} + {x_{2}}^{2} = 4$ ，求m的值．

查看试题解析

23.

某饭店特制了一批高脚杯，分为男士杯和女士杯（如图1），相关信息如下：

素材	内容
素材1	高脚杯：如图1，类似这种杯托上立着一只细长脚的杯子．从下往上分为三部分：杯托，杯脚，杯体．杯托为一个圆；水平放置时候，杯脚经过杯托圆心，并垂直任意直径；杯体的水平横截面都为圆，这些圆的圆心都在杯脚所在直线上．
素材2	图2坐标系中，特制男士杯可以看作线段AB ， OC ，抛物线DCE（实线部分），线段DF ，线段EG绕y轴旋转形成的立体图形（不考虑杯子厚度，下同）．图2坐标系中，特制女士杯可以看作线段AB ， OC ，抛物线FCG（虚线部分）绕y轴旋转形成的立体图形．
素材3	已知，图2坐标系中，OC＝50mm ，记为C（0，50），D（﹣25，75），E（25，75），F（﹣25，150），G（25，150）．

根据以上素材内容，尝试求解以下问题：

(1)、求抛物线DCE和抛物线FCG的解析式；

(2)、当杯子水平放置及杯内液体（无泡沫）静止时，若男士杯中液体与女士杯中液体最深处深度均为30mm ，求两者液体最上层表面圆面积相差多少？（结果保留π）

(3)、当杯子水平放置及杯内液体（无泡沫）静止时，若男士杯中液体与女士杯中液体最深处深度相等，两者液体最上层表面圆面积相差450πmm² ，求杯中液体最深度为多少？

查看试题解析

24. 矩形ABCD中，M ， N分别是边AB ， BC上的两个动点.

(1)、如图，当 DM⊥ MN ， AM=BM时. 求证：①△DAM∽△MBN；②DN=AD+BN.

(2)、当 AB=5，BC=3 时，是否存在点 M的某个位置，使得△DAM∽△MBN∽△DCN ，
若存在，求 AM的长. 若不存在，说明理由.

(3)、是否存在矩形 ABCD ，使得△DAM ， △MBN ， △DCN都和△DMN相似，若存在，求 $\frac{A B}{A D}$ 的值；若不存在，请说明理由.

查看试题解析

类别	频数（人数）	频率
力学	m	0.5
热学	8
光学	20	0.25
电学	12