吉林省长春市宽城区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 如图,数轴上点A表示的数是2023, , 则点B表示的数是( )
 A、2023 B、 C、 D、2. “争创全国文明典范城市,让文明成为长春人民的内在气质和城市的亮丽名片”.一个写有相关宣传标语的正方体的表面展开图如图所示,把展开图折叠成正方体后,“范”字对面的字是( )
A、2023 B、 C、 D、2. “争创全国文明典范城市,让文明成为长春人民的内在气质和城市的亮丽名片”.一个写有相关宣传标语的正方体的表面展开图如图所示,把展开图折叠成正方体后,“范”字对面的字是( )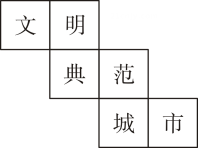 A、文 B、明 C、城 D、市3. 2023年1月17日,国家航天局公布了我国嫦娥五号月球样品的科研成果.科学家们通过对月球样品的研究,精确测定了月球的年龄是20.3亿年,数据20.3亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,张老汉想用长为70米的棚栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈 , 并在边上留一个2米宽的门(建在处,门用其他材料).设的长为米,则下面所列方程正确的是( )
A、文 B、明 C、城 D、市3. 2023年1月17日,国家航天局公布了我国嫦娥五号月球样品的科研成果.科学家们通过对月球样品的研究,精确测定了月球的年龄是20.3亿年,数据20.3亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,张老汉想用长为70米的棚栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈 , 并在边上留一个2米宽的门(建在处,门用其他材料).设的长为米,则下面所列方程正确的是( ) A、 B、 C、 D、5. 如图,在正方形网格中,以点为位似中心,的位似图形可以是( )
A、 B、 C、 D、5. 如图,在正方形网格中,以点为位似中心,的位似图形可以是( )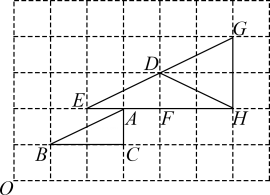 A、 B、 C、 D、6. 我国汉代数学家赵爽在注解《周解算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形面积为25,小正方形面积为1,则的值为( )
A、 B、 C、 D、6. 我国汉代数学家赵爽在注解《周解算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形面积为25,小正方形面积为1,则的值为( )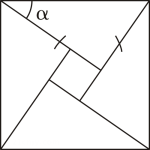 A、 B、 C、 D、7. 如图,四边形是的内接四边形,是的直径,.若.则的大小为( )
A、 B、 C、 D、7. 如图,四边形是的内接四边形,是的直径,.若.则的大小为( )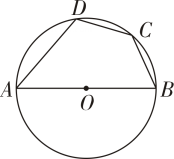 A、 B、 C、 D、8. 如图.在平面直角坐标系中,抛物线交轴的负半轴于点.点是轴负半轴上一点.点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点.若点的横坐标为2,则的长为( )
A、 B、 C、 D、8. 如图.在平面直角坐标系中,抛物线交轴的负半轴于点.点是轴负半轴上一点.点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点.若点的横坐标为2,则的长为( )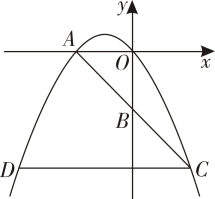 A、4 B、5 C、6 D、8
A、4 B、5 C、6 D、8二、填空题(本大题6小题,每小题3分,共18分)
-
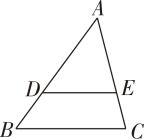
9. 分解因式:.10. 中性笔每支元,铅笔每支元,买5支中性笔和3支铅笔共需元.(用含x、y的代数式表示)11. 若关于x的方程有实数根,则的值可以是.(写出一个即可)12. 如图,在中, , , , 则的值为.
 13. 如图,内接于.若的半径为3, , 则弦的长为.
13. 如图,内接于.若的半径为3, , 则弦的长为.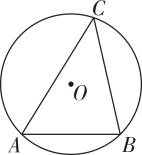 14. 如图,在平面直角坐标系中,抛物线与轴的正半轴交于点.矩形的边在线段上,点C、D在抛物线上,则矩形周长的最大值为.
14. 如图,在平面直角坐标系中,抛物线与轴的正半轴交于点.矩形的边在线段上,点C、D在抛物线上,则矩形周长的最大值为.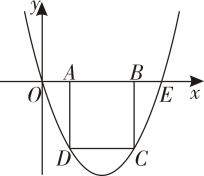
三、解答题(本大题共10小题,共78分)
-
15. 解方程:.16. 小明和小亮对航天知识都非常感兴趣,他们在中国载人航天网站上了解到,航天知识分为“梦圆天路”“飞天英雄”“探秘太空”“巡天飞船”等模块.他们决定先从“梦圆天路”“飞英雄”“探秘太空”三个模块中各随机选择一个进行学习,分别设这三个模块为A、B、C.请用画树状图(或列表)的方法,求小明和小亮选择相同模块的概率.17. 图①、图②、图③均是的正方形网格、每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹,不要求写出画法.
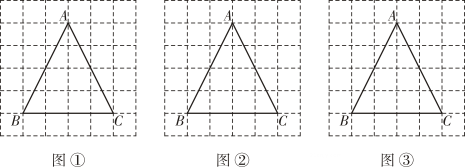 (1)、在图①中的线段上找一点 , 连结 , 使.(2)、在图②中的线段上找一点 , 连结 , 使.(3)、在图③中的内部找一点 , 连结、 , 使.18. 某校为了解本校学生每天在校体育锻炼时间的情况,随机抽取了若干名学生进行调查,获得了他们每天在校体育锻炼时间(单位:分钟)的数据,并对数据进行了整理、描述,部分信息如下.
(1)、在图①中的线段上找一点 , 连结 , 使.(2)、在图②中的线段上找一点 , 连结 , 使.(3)、在图③中的内部找一点 , 连结、 , 使.18. 某校为了解本校学生每天在校体育锻炼时间的情况,随机抽取了若干名学生进行调查,获得了他们每天在校体育锻炼时间(单位:分钟)的数据,并对数据进行了整理、描述,部分信息如下.a.每天在校体育锻炼时间分布情况:
每天在校体育锻炼时间x
频数
百分比
14
14%
40
m
35
35%
n
11%
b.每天在校体育锻炼时间在这一组的是:
80 81 81 81 82 82 83 83 84 84 84 84 84 85 85 85 85 85
85 85 85 86 87 87 87 87 87 88 88 88 89 89 89 89 89
根据以上信息.回答下列问题:
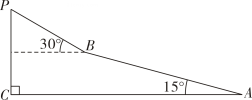
(1)、 , .(2)、该校共有1000名学生,估计该校每天在校体育锻炼时间不低于80分钟的学生人数.(3)、该校准备确定一个时间标准p(单位:分钟),对每天在校体育锻炼时间不低于p分钟的学生进行表扬.若要使25%的学生得到表扬,则p的值可以.19. 某风景区观景缆车路线如图所示,缆车从点出发,途经点后到达山顶 , 其中米,米,且段的运行路线与水平方向的夹角为 , 段的运行路线与水平方向的夹角为 , 求垂直高度.(结果精确到1米)【参考数据: , , 】
 20. 如图,是等腰直角三角形. , 点为的中点,与相切于点 , 连结交于点.
20. 如图,是等腰直角三角形. , 点为的中点,与相切于点 , 连结交于点.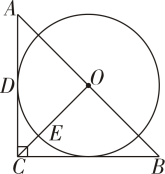 (1)、判断所在直线与的位置关系,并说明理由.(2)、若的半径为2,求的长.(结果保留)21. 已知乒乓球桌的长度为 , 某人从球桌边缘正上方高处将乒乓球向正前方抛向对面桌面,乒乓球的运动路线近似是抛物线的一部分.建立如图所示的平面直角坐标系,设乒乓球离桌面的竖直高度为 , 离球桌边缘的水平距离为.
(1)、判断所在直线与的位置关系,并说明理由.(2)、若的半径为2,求的长.(结果保留)21. 已知乒乓球桌的长度为 , 某人从球桌边缘正上方高处将乒乓球向正前方抛向对面桌面,乒乓球的运动路线近似是抛物线的一部分.建立如图所示的平面直角坐标系,设乒乓球离桌面的竖直高度为 , 离球桌边缘的水平距离为.
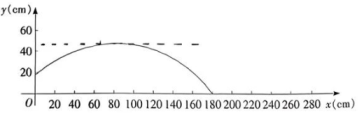 (1)、从乒乓球抛出到第一次落在球桌的过程中,与近似满足函数关系.
(1)、从乒乓球抛出到第一次落在球桌的过程中,与近似满足函数关系.与的几组数据如下表所示:
水平距离x(cm)
0
40
80
120
160
180
竖直高度y(cm)
18
42
50
42
18
0
根据表中数据,直接写出乒乓球离桌面竖直高度的最大值,并求出满足的函数关系式.
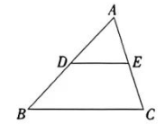
(2)、乒乓球第一次落在球桌后弹起,它离桌面的竖直高度与离球桌边缘的水平距离近似满足函数关系 , 通过计算说明乒乓球再次落下时是否仍落在球桌上.22. 三角形的中位线是非常重要的数学概念,其性质及应用蕴含着丰富的数学思想方法,可以解决诸多数学问题.图①
 图②
图② 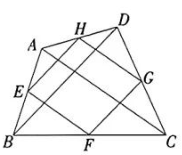 图③
图③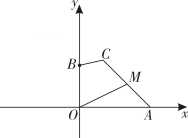 (1)、如图①,在中,点D、E分别为、的中点.连结 , 则线段与的位置关系与数量关系分别为 , .(2)、如图②,在四边形中,点E、F、G、H分别为、、、的中点.连结、 , 且 , 求四边形的周长.(3)、如图③,在平面直角坐标系中,点A、B的坐标分别为 , 点是坐标平面内一点,且.点是线段的中点,连结 , 则线段长度的最大值为.23. 如图,在中, , , .点在边上运动,点关于点的对称点为点 , 以为边在上方作正方形.设.
(1)、如图①,在中,点D、E分别为、的中点.连结 , 则线段与的位置关系与数量关系分别为 , .(2)、如图②,在四边形中,点E、F、G、H分别为、、、的中点.连结、 , 且 , 求四边形的周长.(3)、如图③,在平面直角坐标系中,点A、B的坐标分别为 , 点是坐标平面内一点,且.点是线段的中点,连结 , 则线段长度的最大值为.23. 如图,在中, , , .点在边上运动,点关于点的对称点为点 , 以为边在上方作正方形.设. (1)、的长为.(2)、求线段的长.(用含x的代数式表示)(3)、当正方形与重叠部分的图形为四边形时,求的取值范围.(4)、连结 , 当所在直线将正方形的面积分成1:2两部分时,直接写出的值.24. 在平面直角坐标系中,二次函数(b、c为常数)的图象经过点和点.(1)、求这个二次函数的表达式.(2)、当时,二次函数的最大值与最小值的差为1,求的取值范围.(3)、当时,设二次函数的最大值与最小值的差为 , 求与之间的函数关系式.(4)、点在直线上运动,若在坐标平面内有且只有两个点使为直角三角形,直接写出的取值范围.
(1)、的长为.(2)、求线段的长.(用含x的代数式表示)(3)、当正方形与重叠部分的图形为四边形时,求的取值范围.(4)、连结 , 当所在直线将正方形的面积分成1:2两部分时,直接写出的值.24. 在平面直角坐标系中,二次函数(b、c为常数)的图象经过点和点.(1)、求这个二次函数的表达式.(2)、当时,二次函数的最大值与最小值的差为1,求的取值范围.(3)、当时,设二次函数的最大值与最小值的差为 , 求与之间的函数关系式.(4)、点在直线上运动,若在坐标平面内有且只有两个点使为直角三角形,直接写出的取值范围.