吉林省通化市梅河口市2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 若方程 $(m + 1) x^{2} + 4 x + 9 = 0$ 是关于 $x$ 的一元二次方程，则 $m$ 的取值范围是（）

A、 $m > - 1$ B、 $m < - 1$ C、 $m \neq - 1$ D、 $m$ 为任意实数

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，是必然事件的是（）

A、今年冬季兴城的最低气温为40℃ B、下午考试，小明会考满分 C、乘坐公共汽车恰好有空座 D、四边形的内角和是360°

查看试题解析
4. 在一个不透明的袋子里装有除颜色外完全相同的若干个黑球和白球，小红摸出一个小球记录颜色后放回口袋，经过大量的摸球试验后发现摸到白球的频率稳定在0.2左右，那么摸出黑球的概率约为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
5. 如图， $B C$ 为 $⊙ O$ 直径，点A，D在 $⊙ O$ 上， $∠ D A B = 135 °$ ，若 $B C = 4$ ，则 $C D$ 的长为（）

A、2 B、1 C、 $2 \sqrt{2}$ D、 $\sqrt{2}$

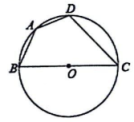查看试题解析
6. 电影《我和我的祖国》一上映就受到观众热烈追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元．若设增长率为x，则根据题意可列方程为（）

A、 $3 (1 + x) = 10$ B、 $3 {(1 + x)}^{2} = 10$ C、 $3 + 3 {(1 + x)}^{2} = 10$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 10$

查看试题解析
7. 如图， $△ A B C$ 中，点 $D$ 在线段 $A C$ 上，连接 $B D$ ，要使 $△ A B D$ 与 $△ A B C$ 相似，只需添加一个条件即可，这个条件不能是（）

A、 $\frac{A D}{A B} = \frac{B D}{B C}$ B、 $∠ A D B = ∠ A B C$ C、 $∠ A B D = ∠ C$ D、 $A B^{2} = A D \cdot A C$

查看试题解析
8. 将二次函数 $y = 2 x^{2} + 4 x - 1$ 的图象向上平移，得到的函数图象与 $x$ 轴只有一个公共点，则平移的距离为（）

A、1个单位长度 B、2个单位长度 C、3个单位长度 D、4个单位长度

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的图象上部分点的横坐标 $x$ 和纵坐标 $y$ 的对应值如下表：
$x$
…
1
3
4
5
…
$y$
…
9
1
3
9
…
下列结论正确的是（）

A、开口向下 B、 $4 a + 2 b + c = 3$ C、对称轴是 $x = 3.5$ D、若 $A (6 ， y_{1})$ 和 $B (- 6 ， y_{2})$ 是抛物线上两点，则 $y_{1} > y_{2}$

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为4， $△ E F G$ 中， $E F = E G = \sqrt{17}$ ， $F G = 2$ ， $B C$ 和 $F G$ 在一条直线上，当 $△ E F G$ 从点 $G$ 和点 $B$ 重合时开始向右平移，直到点 $F$ 与点 $C$ 重合时停止运动，设 $△ E F G$ 平移的距离为 $x$ ， $△ E F G$ 与正方形 $A B C D$ 重叠部分的面积为 $y$ ，则下列图象中能大致反映 $y$ 与 $x$ 的函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共8个小题，每小题3分，共24分）

11. 在平面直角坐标系中，将点 $A (- 3 ， 2)$ 绕原点 $O$ 逆时针旋转180°得到点 $A^{'}$ ，则点 $A^{'}$ 的坐标是；

查看试题解析
12. 若一元二次方程 $2 x^{2} - 3 x + c = 0$ 无解，则c的取值范围为．

查看试题解析
13. 半径为10cm的半圆围成一个圆锥，则这个圆锥的高是cm．

查看试题解析
14. 某种礼炮的升空高度 $h (m)$ 与飞行时间 $t (s)$ 的关系式是 $h = - \frac{5}{2} t^{2} + 30 t + 1$ ，则这种礼炮在点火升空到最高点引爆，则从点火升空到引爆需要的时间为s；

查看试题解析
15. 如图，点C，D在 $⊙ O$ 上直径 $A B$ 两侧的两点， $∠ A C D = 60 °$ ， $A B = 8$ ，则 $\overset{⌢}{B D}$ 的长为；

查看试题解析
16. 如图，点 $C$ 在线段 $A B$ 上， $A C = 1$ ， $B C = 2$ ，以 $A C$ 为边作正方形 $A C E D$ ，连接 $B D$ 交 $C E$ 于点 $F$ ，则 $△ D E F$ 的面积为：

查看试题解析
17. 如图， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C = 4$ ，点 $D$ 在线段 $B C$ 上， $B D = 3 \sqrt{2}$ ，线段 $A D$ 绕点 $A$ 逆时针旋转90°得到线段AE ， $E F ⊥ A C$ ，垂足为点F ，则EF的长为；

查看试题解析
18. 如图，四边形 $A B C D$ 是正方形，点E在 $C B$ 的延长线上，连接 $A E$ ， $A F ⊥ A E$ 交 $C D$ 于点F，连接 $E F$ ，点H是 $E F$ 的中点，连接 $B H$ ，则下列结论中：① $B E = D F$ ；② $∠ B E H = ∠ B A H$ ；③ $\frac{B H}{C F} = \frac{\sqrt{2}}{2}$ ；④若 $A B = 4 ， D F = 1$ ，则 $△ B E H$ 的面积为 $\frac{3}{2}$ ．正确的是（填写所有正确结论的序号）．

查看试题解析

三、解答题（第19题10分，第20题12分，共22分）

19. 解方程：

(1)、 $x^{2} - 2 x - 6 = 0$ ；

(2)、 $(x + 4)^{2} = 5 (x + 4)$ ；

查看试题解析
20. 如图，在平面直角坐标系中， $△ O A B$ 的三个顶点的坐标分别为 $O (0 ， 0)$ ， $A (5 ， 3)$ ， $B (0 ， 5)$ .

(1)、画出 $△ O A B$ 绕原点O逆时针方向旋转90°后得到的 $△ O A_{1} B_{1}$ ；

(2)、连接 $A A_{1}$ ， $∠ O A A_{1}$ 的度数为°；

(3)、以原点O为位似中心，相似比为 $\frac{1}{2}$ ，在第一象限内将 $△ A B O$ 缩小得到 $△ A_{2} B_{2} O$ ，画出 $△ A_{2} B_{2} O$ ，直接写出点 $A_{2}$ 的坐标.

查看试题解析

四、解答题（每题12分，共24分）

21. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中选出一类最喜爱的电视节目，以下是根据调查结果绘制的统计图表的一部分.

类别	A	B	C	D	E
类型	新闻	体育	动画	娱乐	戏曲
人数	11	20	40	m	4

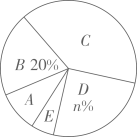
请你根据以上信息，回答下列问题：

(1)、统计表中m的值为，统计图中n的值为， A类对应扇形的圆心角为度；

(2)、该校共有1500名学生，根据调查结果，估计该校最喜爱体育节目的学生人数；

(3)、样本数据中最喜爱戏曲节目的有4人，其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演，请用树状图或列表求所选2名同学中有男生的概率.

查看试题解析

22. 在体育测试中，九年级的一名男生推铅球，已知铅球经过的路线是某个二次函数图象的一部分，如图所示，如果这个男生的出手处A点的坐标是 $(0 ， 2)$ ，铅球路线的最高处B点的坐标是 $(4 ， \frac{8}{3})$ .

(1)、求这个二次函数的解析式；

(2)、该男生能把铅球推出去多远.

查看试题解析

五、解答题（满分12分）

23. 某市政府大力扶持大学生创业，小明在政府的扶持下投资销售一种进价为每千克6元的农产品.销售过程中发现，每天的销售量 $y$ （千克）与销售单价 $x$ （元）之间满足一次函数关系，部分数据如下表所示，另外在销售过程中小明每天需要支付其他费用200元.
销售单价 $x$ （元/千克）
10
11
销售量 $y$ （千克）
300
270

(1)、求 $y$ 与 $x$ 的函数关系式：

(2)、根据物价部门的规定，这种农产品的销售单价不得高于12元，那么如何定价才能使小明每天获得的纯利润最大？最大纯利润是多少元？

查看试题解析

六、解答题（满分12分）

24. 如图，四边形ABOD是平行四边形，以O为圆心，OB为半径的圆经过点A ，延长 $B O$ 交 $⊙ O$ 于点E ， $\overset{⌢}{A B} = \overset{⌢}{A E}$ ，连接DE.

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $A B = \sqrt{2}$ ，求图中阴影部分面积.

查看试题解析

七、解答题（满分12分）

25. 已知 $△ A B C$ 和 $△ A D E$ 中， $∠ B A C = ∠ D A E = 60 °$ ， $∠ A C B = ∠ A E D = α °$ ，连接CE、CD ，点F、G分别为CD和BC的中点，连接FG.

(1)、如图1，当 $α = 60 °$ 时，FG与EC的数量关系是；

(2)、如图2，当 $α = 90 °$ 时，
①请判断FG与EC的数量关系，并说明理由：
②若 $A C = 5$ ， $A E = 2$ ，将 $△ A D E$ 绕点A旋转一周，在旋转的过程中，当点B，D，E在一条直线上时，请直接写出线段EC的长.

查看试题解析

八、解答题

26. 如图，平面直角坐标系中，抛物线 $y = a x^{2} + b x + 3$ 与 $x$ 轴交于点 $A (- 3 ， 0)$ 和 $B (1 ， 0)$ ，与 $y$ 轴交于点 $C$ ，点 $D$ 是抛物线的顶点，连接AD，AC.

(1)、求抛物线的解析式；

(2)、如图1，点E在线段CO上，连接AE ，当 $∠ E A C = ∠ D A C$ 时，求点E的坐标；

(3)、如图2，将 $△ A O C$ 沿直线 $A C$ 平移得到 $△ A_{1} O_{1} C_{1}$ ，连接 $C_{1} B$ ， $A_{1} B$ ，在平移过程中是否存在点 $A_{1}$ ，使 $△ A_{1} B C_{1}$ 是等腰三角形，若存在，请直接写出点 $A_{1}$ 的坐标；若不存在，请说明理由.

查看试题解析

销售单价 $x$ （元/千克）	10	11
销售量 $y$ （千克）	300	270

$x$	…	1	3	4	5	…
$y$	…	9	1	3	9	…