吉林省松原市长岭县2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. ( )A、6 B、 C、 D、2. 国庆假期,各旅游景区节庆氛围浓厚.某景区同步设置的“我为祖国点赞”装置共收集约6390000个“赞”,这个数字用科学记数法可表示为( )A、 B、 C、 D、3. 设某数是x , 若比它的2倍大4的数是8,则可列方程为( )A、 B、 C、 D、4. 若与是同类项,则的值为( )A、2 B、3 C、6 D、95. 若是关于x的一元一次方程,则m的值为( )A、1 B、2 C、3 D、1或36. 由5个大小相同的正方体组成的立体图形如图所示,从前面看到的平面图形是( )
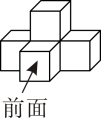 A、
A、 B、
B、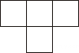 C、
C、 D、
D、 7. 下列计算正确的是( ).A、 B、 C、 D、8. 下列式子是根据等式的性质进行变形的,其中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 如图,将一张长方形纸片斜折过去,使顶点A落在处,为折痕,然后再把折过去,使之与重合,折痕为 . 若 , 则的度数为( )
7. 下列计算正确的是( ).A、 B、 C、 D、8. 下列式子是根据等式的性质进行变形的,其中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 如图,将一张长方形纸片斜折过去,使顶点A落在处,为折痕,然后再把折过去,使之与重合,折痕为 . 若 , 则的度数为( )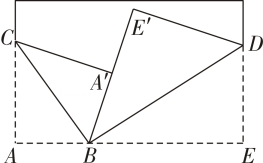 A、 B、 C、 D、10. 观察下列图形中各数之间的规律,根据观察到的规律得出n的值为( )
A、 B、 C、 D、10. 观察下列图形中各数之间的规律,根据观察到的规律得出n的值为( ) A、241 B、113 C、143 D、271
A、241 B、113 C、143 D、271二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 若m是的相反数,则m的值为 .12. 若单项式的次数是5,则n的值为 .13. 若 , 则的补角为 .14. 若是关于x的方程的解,则a的值为 .15. 定义一种新运算▽:对任意有理数a , b都有 , 如 , 则 .
三、解答题(本大题共8个小题,共75分)
-
16. 计算:(1)、;(2)、 .17. 解方程:(1)、;(2)、 .18. 如图,已知线段a和线段 .
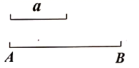 (1)、尺规作图:延长线段 到C,使 (不写作法,保留作图痕迹);(2)、在(1)的条件下,若 , ,取线段 的中点O,求线段 的长.19. 先化简,再求值. .其中 , .20. 如图,点O是直线上一点,以点O为顶点作 , 且 , 位于直线两侧,平分 .
(1)、尺规作图:延长线段 到C,使 (不写作法,保留作图痕迹);(2)、在(1)的条件下,若 , ,取线段 的中点O,求线段 的长.19. 先化简,再求值. .其中 , .20. 如图,点O是直线上一点,以点O为顶点作 , 且 , 位于直线两侧,平分 .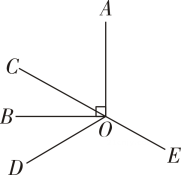 (1)、当时,求的度数;(2)、请你猜想和的数量关系,并说明理由.21. 为提高学生保护环境的意识,某班开展了环保知识竞赛.学习委员为班级购买奖品后与生活委员的对话如下:
(1)、当时,求的度数;(2)、请你猜想和的数量关系,并说明理由.21. 为提高学生保护环境的意识,某班开展了环保知识竞赛.学习委员为班级购买奖品后与生活委员的对话如下: (1)、请用方程的知识计算一下,为什么说学习委员算错了?(2)、学习委员连忙拿出发票,发现的确错了.因为他还买了一本笔记本,但笔记本的单价已模糊不清,只记得是2元或3元,那么笔记本的单价是多少元?
(1)、请用方程的知识计算一下,为什么说学习委员算错了?(2)、学习委员连忙拿出发票,发现的确错了.因为他还买了一本笔记本,但笔记本的单价已模糊不清,只记得是2元或3元,那么笔记本的单价是多少元?