吉林省长春市农安县2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 立方根为( )A、 B、 C、 D、2. 在下列实数中,无理数是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 若是完全平方式,则k的值是( )A、 B、 C、3 D、65. 如图所示,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
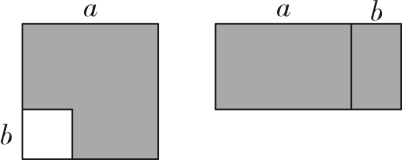 A、 B、 C、 D、6. 在下列各命题中,是假命题的是( )A、在一个三角形中,等边对等角 B、全等三角形的对应边相等 C、同旁内角相等,两直线平行 D、等角的补角相等7. 如图,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点D,作射线 , 则说明的依据是( )
A、 B、 C、 D、6. 在下列各命题中,是假命题的是( )A、在一个三角形中,等边对等角 B、全等三角形的对应边相等 C、同旁内角相等,两直线平行 D、等角的补角相等7. 如图,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点D,作射线 , 则说明的依据是( )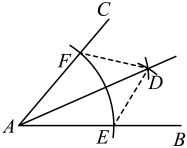 A、 B、 C、 D、8. 下列三角形中,不是直角三角形的是( )A、中, B、中, , C、中, D、中,三边之比为9. 等腰三角形的腰长为5,底边上的中线长为4,它的面积为( )A、24 B、20 C、15 D、1210. 如图,中, , 平分 , , , 则的面积为( )
A、 B、 C、 D、8. 下列三角形中,不是直角三角形的是( )A、中, B、中, , C、中, D、中,三边之比为9. 等腰三角形的腰长为5,底边上的中线长为4,它的面积为( )A、24 B、20 C、15 D、1210. 如图,中, , 平分 , , , 则的面积为( )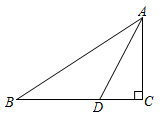 A、20 B、10 C、15 D、30
A、20 B、10 C、15 D、30二、填空题(每小题4分,共40分)
-
11. 若 , 则12. 分解因式: .13. “若 , 则 , ”是命题(选填“真”或“假”).14. 已知直角三角形两直角边长分别为3和5,则斜边长为 .15. 用反证法证明命题“在一个三角形中,不能有两个内角为钝角”时,第一步应假设 .16. 为了解某市4万名学生平均每天读书的时间,请你运用数学的统计知识将统计的主要步骤进行排序:
①得出结论,提出建议;
②分析数据;
③从4万名学生中随机抽取400名学生,调查他们平均每天读书的时间;
④利用统计图表将收集的数据整理和表示。
合理的排序是.
17. 如图,将一张长方形纸片ABCD按图中那样折叠,若 , , , 则重叠部分(阴影)的面积是.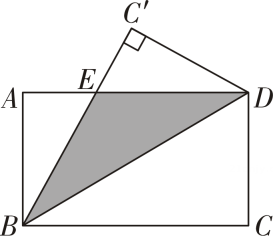 18. 如图,赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形 , 若 , , 则中间小正方形的面积是 .
18. 如图,赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形 , 若 , , 则中间小正方形的面积是 .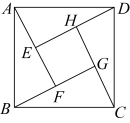 19. 如图,在中,的中垂线交边于点 , , , 则.
19. 如图,在中,的中垂线交边于点 , , , 则.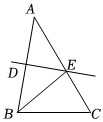 20. 若的三边长分别为 , 7,6,当为等腰三角形时,则a的值为 .
20. 若的三边长分别为 , 7,6,当为等腰三角形时,则a的值为 .三、解答题(21-24题各5分,25、26题各7分,27、28题各8分,共50分)
-
21. 已知实数的一个平方根是-5,的立方根是-2,求的算术平方根.22. 先化简,再求值: , 其中.23. 已知 , , 求与的值.24. 如图,已知 , , , , .求图中着色部分的面积.
 25. 图①、图②、图③均是6×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,的顶点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上.
25. 图①、图②、图③均是6×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,的顶点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上. (1)、在图①中以AC为边,画一个等腰;(2)、在图②中画 , 使与关于直线AB对称;(3)、在图③中画 , 使全等.26. 为了解某校九年级学生数学期末考试情况,小亮随机抽取了部分学生的数学成绩(成绩都为整数)为样本,分为A(90~100分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果制成如下统计图,请根据图中信息解答以下问题:
(1)、在图①中以AC为边,画一个等腰;(2)、在图②中画 , 使与关于直线AB对称;(3)、在图③中画 , 使全等.26. 为了解某校九年级学生数学期末考试情况,小亮随机抽取了部分学生的数学成绩(成绩都为整数)为样本,分为A(90~100分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果制成如下统计图,请根据图中信息解答以下问题: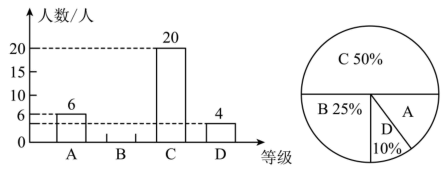 (1)、求这次随机抽取的样本容量;(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?27. 阅读下列材料:
(1)、求这次随机抽取的样本容量;(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?27. 阅读下列材料:因式分解的常用方法有提取公因式法和公式法,但有的多项式仅用上述方法就无法分解,如 . 我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:
. 这种因式分解的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
(1)、因式分解:;(2)、三边 , , 满足 , 判断的形状并说明理由.28. (1)、如图1,与均是顶角为40°的等腰三角形,BC、DE分别是底边,
(1)、如图1,与均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:;
(2)、如图2,和均为等边三角形,点A、D、E在同一直线上,连接BE.填空:的度数为;线段BE与AD之间的数量关系是.
(3)、拓展探究如图3,和均为等腰直角三角形, , 点A、D、E在同一直线上,CM为中DE边上的高,连接BE.求线段CM、AE、BE之间的数量关系,并说明理由.