吉林省吉林市蛟河市三校联考2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(每小题2分,共12分)
-
1. 下列标志中,可以看作是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列各图中,正确画出AC边上的高的是( )A、
2. 下列各图中,正确画出AC边上的高的是( )A、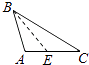 B、
B、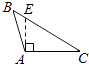 C、
C、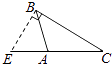 D、
D、 3. 如果a﹣b=4,ab=6,那么ab2﹣a2b的值是( )A、﹣24 B、﹣10 C、24 D、24. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
3. 如果a﹣b=4,ab=6,那么ab2﹣a2b的值是( )A、﹣24 B、﹣10 C、24 D、24. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )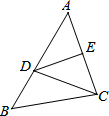 A、50° B、100° C、120° D、130°5. 已知点P(m﹣1,4)与点Q(2,n+2)关于y轴对称,则nm的值为( )A、﹣2 B、 C、﹣ D、16. 某化肥厂原计划每天生产化肥x吨,由于采取了新技术,每天多生产化肥3吨,实际生产180吨与原计划生产120吨的时间相等,那么适合x的方程是( )A、 B、 C、 D、
A、50° B、100° C、120° D、130°5. 已知点P(m﹣1,4)与点Q(2,n+2)关于y轴对称,则nm的值为( )A、﹣2 B、 C、﹣ D、16. 某化肥厂原计划每天生产化肥x吨,由于采取了新技术,每天多生产化肥3吨,实际生产180吨与原计划生产120吨的时间相等,那么适合x的方程是( )A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 计算:|﹣2023|= .8. 因式分解:3x2﹣9x= .9. 计算的结果为 .10. 如图,AB,CD相交于点O,AD=CB,请你补充一个条件,使得△ABD≌△CDB,你补充的条件是 .
 11. 如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米.
11. 如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米. 12. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,S△ABC=15,DE=3,AB=6,则AC长是 .
12. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,S△ABC=15,DE=3,AB=6,则AC长是 . 13. 如图,等边三角形ABC中,点F,E分别在AB,BC上,CD=1,把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.若∠AFD=90°,则CE= .
13. 如图,等边三角形ABC中,点F,E分别在AB,BC上,CD=1,把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.若∠AFD=90°,则CE= . 14. 小明家离学校2000米,小明平时从家到学校需要用x分钟,今天起床晚,怕迟到,走路速度比平时快5米/分钟,结果比平时少用了2分钟到达学校,则根据题意可列方程 .
14. 小明家离学校2000米,小明平时从家到学校需要用x分钟,今天起床晚,怕迟到,走路速度比平时快5米/分钟,结果比平时少用了2分钟到达学校,则根据题意可列方程 .三、解答题(每小题5分,共20分)
-
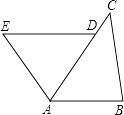
15. 分解因式:﹣x3﹣2x2﹣x.16. [(x+y)2﹣(x+y)(x﹣y)]÷2y.17. 已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.
 18. 解方程: = .
18. 解方程: = .四、解答题(每小题7分,共28分)
-
19. 已知多项式A=(x+2)2+(1﹣x)(2+x)﹣3.(1)、化简多项式A;(2)、若(x+1)2=6,求A的值.20.
已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
 (1)、在坐标系内描出点A、B、C的位置,并求△ABC的面积
(1)、在坐标系内描出点A、B、C的位置,并求△ABC的面积
(2)、在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标
(3)、若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.21. 如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.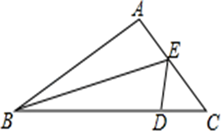 (1)、求证:△ABE≌△DBE;(2)、若∠A=100°,∠C=50°,求∠AEB的度数.22. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.设马小虎的速度为x米/分.(1)、依题意,填写下表:
(1)、求证:△ABE≌△DBE;(2)、若∠A=100°,∠C=50°,求∠AEB的度数.22. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.设马小虎的速度为x米/分.(1)、依题意,填写下表:路程
速度
时间
小虎
x
爸爸
1600
2x
(2)、根据上表,列方程解决问题.五、解答题(每小题8分,共16分)
-
23. 如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
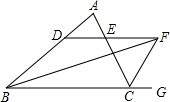
问:
(1)、图中有几个等腰三角形?为什么?(2)、BD,CE,DE之间存在着什么关系?请证明.24. 观察下列方程的特征及其解的特点;①x+=﹣3的解为x1=﹣1,x2=﹣2.
②x+=﹣5的解为x1=﹣2,x2=﹣3.
③x+=﹣7的解为x1=﹣3,x2=﹣4;
解答下列问题;
(1)、请你写出一个符合上述特征的方程为 , 其解为 .(2)、根据这类方程特征,写出第n个方程为 , 其解为 .(3)、请利用(2)的结论,求关于x的方程x+=﹣2(n+2)(其中n为正整数)的解.六、解答题(每小题10分,共20分)
-
25. 如图,将边长为a的正方形按虚线剪成4个部分,去掉其中边长为b的小正方形,将剩余的3个部分重新拼成一个互不重叠且无缝隙的长方形.
 (1)、画出拼好的长方形,并标注相应的数据;(2)、求拼好后长方形的周长;(3)、若a=9,b=3,求拼好后长方形的面积.26. 问题背景:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.
(1)、画出拼好的长方形,并标注相应的数据;(2)、求拼好后长方形的周长;(3)、若a=9,b=3,求拼好后长方形的面积.26. 问题背景:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC. (1)、探究一:当∠BAE=90°时.
(1)、探究一:当∠BAE=90°时.①若∠B=45°,求∠DAC的度数;
②若∠B=α°,则∠CAE的度数用含α的式子表示为 ▲ °,∠CAD的度数为 ▲ °.
(2)、探究二:若∠BAE=n°,直接写出∠DAC的度数.