吉林省四平市铁西区2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、单项选择题(每小题2分,共12分)
-
1. 下列几种著名的数学曲线中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式中计算结果等于的是( )A、 B、 C、 D、3. 若分式 在实数范围内有意义,则实数x的取值范围是( )A、 B、 C、 D、4. 如图,点 , 分别在线段 , 上,与相交于点,已知 , 现添加以下的哪个条件仍不能判定的是( )
2. 下列各式中计算结果等于的是( )A、 B、 C、 D、3. 若分式 在实数范围内有意义,则实数x的取值范围是( )A、 B、 C、 D、4. 如图,点 , 分别在线段 , 上,与相交于点,已知 , 现添加以下的哪个条件仍不能判定的是( ) A、 B、 C、 D、5. 已知是完全平方式,则为( )A、 B、 C、6 D、126. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、
A、 B、 C、 D、5. 已知是完全平方式,则为( )A、 B、 C、6 D、126. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、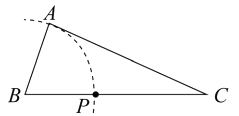 B、
B、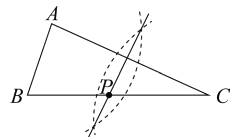 C、
C、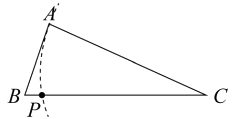 D、
D、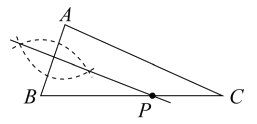
二、填空题(每小题3分,共24分)
-
7. 冬季是流感的高发季节,某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示 .8. 已知a,b,c是的三边长,满足 , c为奇数,则 .9. 若等腰三角形的两边长分别是3和6,则它的周长为 .10. 已知关于的方程无解,则 .11. 已知x +y=5 ,xy=6 ,则x2 + y2=.12. 下列各式:①;②;③;④ , 能用公式法分解因式的是(填序号).13. 如图,点在上,于点 , 交于点 , , . 若 , 则°.
 14. 如图,D为内一点,平分 , , 垂足为D,交与点E, . 若 , , 则的长为 .
14. 如图,D为内一点,平分 , , 垂足为D,交与点E, . 若 , , 则的长为 .
三、解答题(每小题5分,共20分)
-
15. 计算: .16. 因式分解: .17. 解方程:18. 解方程: .
四、解答题(每题7分,共28分)
-
19. 先化简 ,再在1,2,3中选取一个适当的数代入求值.20. 若一个多边形的内角和的比它的外角和多 , 那么这个多边形的边数是多少?21. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、均为格点,只用无刻度的直尺,分别在给定的三幅图中画出点 , 使点在线段上,且满足以下要求,保留适当的作图痕迹.
 (1)、在图①中,连结 , 使最小;(2)、在图②中,连结、 , 使;(3)、在图③中,连结、 , 使最小.22. 如图, , , 于 , 于 , , .
(1)、在图①中,连结 , 使最小;(2)、在图②中,连结、 , 使;(3)、在图③中,连结、 , 使最小.22. 如图, , , 于 , 于 , , . (1)、求证:;(2)、请直接写出的长.
(1)、求证:;(2)、请直接写出的长.五、解答题(每题8分,共16分)
-
23. 阅读材料:
=( ▲ )
= ▲ .
(1)、请把阅读材料补充完整;(2)、分解因式:;(3)、已知 , , 为的三边长,若 , 试判断的形状,并说明理由.24. 如图,已知: , 点是内一点, , , 点是延长线上一点,在线段上截取 , 连接 . (1)、求的度数;(2)、求证: .
(1)、求的度数;(2)、求证: .六、解答题(每题10分,共20分)
-
25. 我国已成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势,经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元,若充电费和加油费均为300元时,电动汽车可行驶的总路程是燃油车的4倍,设这款电动汽车平均每公里的充电费用为元.(1)、当充电费为300元时,这款电动汽车的行驶路程为公里(用含的代数式表示);(2)、请分别求出这两款车的平均每公里的行驶费用;(3)、若燃油车和电动汽车每年的其它费用分别为4800元和7800元,问每年行驶里程在什么范围时,买电动汽车的年费用更低?(年费用=年行驶费用+年其它费用)26. 长方形中, , , 点以每秒1个单位的速度从向运动,点同时以每秒2个单位的速度从向运动,设 , 两点运动时间为 , 点为边上任意一点.(点不与点、点重合)
 (1)、请直接用含、的代数式,表示线段的长度;(2)、当时,连接 , 若与全等,求的长;(3)、若在边上总存在点使得 , 请直接写出的取值范围.
(1)、请直接用含、的代数式,表示线段的长度;(2)、当时,连接 , 若与全等,求的长;(3)、若在边上总存在点使得 , 请直接写出的取值范围.