吉林省长春市二道区2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. ﹣2024的相反数是( )A、﹣2024 B、2024 C、±2024 D、2. 2023年9月23日第19届亚运会在我国杭州举行,截至10月7日,杭州亚运会官方宣布票务收入超610000000元人民币,其中610000000这个数用科学记数法表示为( )A、0.61×109 B、6.1×109 C、6.1×107 D、6.1×1083. 如图所示的几何体是由5个完全相同的小正方体搭成的,从它的左面看到的平面形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 若∠A=62°45',则∠A的补角的度数为( )A、27°55' B、137°15' C、117°15' D、117°55'5. 小红同学通过对《有理数的乘方》的学习发现:2的乘方结果的个位数有一定的规律“21=2,22=4,23=8,24=16,25=32,⋯⋯”,请你推算250的个位数是( )A、2 B、4 C、6 D、86. 如图,点C是线段AB上的点,点D是线段AB的中点.若AB=8,BC=5,则CD的长度为( )
4. 若∠A=62°45',则∠A的补角的度数为( )A、27°55' B、137°15' C、117°15' D、117°55'5. 小红同学通过对《有理数的乘方》的学习发现:2的乘方结果的个位数有一定的规律“21=2,22=4,23=8,24=16,25=32,⋯⋯”,请你推算250的个位数是( )A、2 B、4 C、6 D、86. 如图,点C是线段AB上的点,点D是线段AB的中点.若AB=8,BC=5,则CD的长度为( ) A、1 B、2 C、3 D、47. 下列图形中,和是同位角的是( )A、
A、1 B、2 C、3 D、47. 下列图形中,和是同位角的是( )A、 B、
B、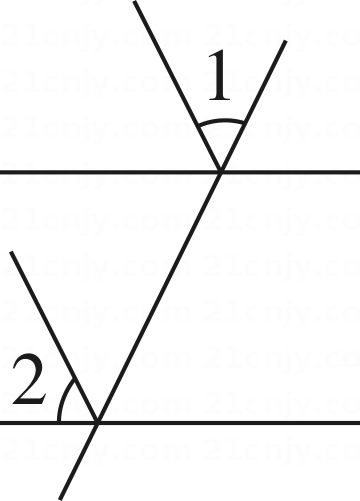 C、
C、 D、
D、 8. 如图所示是一个计算机程序图,如果开始输入x=0,那么最后输出的结果为( )
8. 如图所示是一个计算机程序图,如果开始输入x=0,那么最后输出的结果为( ) A、﹣2 B、1 C、﹣5 D、﹣1
A、﹣2 B、1 C、﹣5 D、﹣1二、填空题(本大题共6小题,每小题3分,共18分)
-
9. 某天早晨的气温是﹣13℃,到中午升高了5℃,则中午时的温度为 ℃.10. 若某三位数的个位数字为a,十位数字为b,百位数字为c,则这个三位数可表示为 .11. 若与的和是单项式,则a+2b的值为 .12. 建筑工人在砌墙时,经常在两个墙角分别立一根标志杆,在两根标志杆之间拉一条线,沿这条线就可以砌出直的墙了,其中的数学道理是 .
 13. 如图,有A、B、C三个城市,城市B在城市A的南偏东56°方向,城市C在城市B的北偏东23°方向,那么∠ABC的大小为 度.
13. 如图,有A、B、C三个城市,城市B在城市A的南偏东56°方向,城市C在城市B的北偏东23°方向,那么∠ABC的大小为 度. 14. 如图,光线在不同介质中的传播速度是不同的,因此当光线从空气射向水中时,要发生折射.由于折射率相同,所以在空气中平行的光线,在水中也是平行的.若∠1=56°,∠2=112°,则∠3的大小为 度.
14. 如图,光线在不同介质中的传播速度是不同的,因此当光线从空气射向水中时,要发生折射.由于折射率相同,所以在空气中平行的光线,在水中也是平行的.若∠1=56°,∠2=112°,则∠3的大小为 度.
三、解答题(本大题共10小题,共78分)
-
15. 计算: .16. 先化简,再求值:(2x2y+xy)﹣(x2y﹣5xy)+2x2y,其中x=2,y=﹣1.17. 在如图所示的方格中,点A、B、C均为网格点,按要求画图并回答问题:
 (1)、画直线AC.(2)、过点C画线段AB的垂线,垂足为点D.(3)、点C与直线AB上各点连结的所有线段中,线段CD最短的数学道理是____.A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短18. 某检修小组乘一辆汽车沿东西方向的公路检修线路,约定向东为正,某天这辆汽车从A地出发到收工时,行走记录为(单位:千米):
(1)、画直线AC.(2)、过点C画线段AB的垂线,垂足为点D.(3)、点C与直线AB上各点连结的所有线段中,线段CD最短的数学道理是____.A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短18. 某检修小组乘一辆汽车沿东西方向的公路检修线路,约定向东为正,某天这辆汽车从A地出发到收工时,行走记录为(单位:千米):+15、﹣2、+5、﹣1、﹣3、﹣2.+12、+4、﹣5、+6.
(1)、计算收工时,汽车在A地的哪一边,距A地多远?(2)、计算这辆汽车一共走了多少千米?(3)、若每千米汽车耗油量为0.8升,求出发到收工汽车耗油多少升?19. 如图,射线OA在∠BOC内部,OM平分∠AOB,ON平分∠AOC. (1)、若∠AOB=90°,∠AOC=20°,求∠MON的度数.(2)、若∠AOB=x°,∠AOC=y°,则∠MON的大小为 度.(用含x、y的代数式表示)20. 如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?完成下面解答过程中的填空或填写理由.
(1)、若∠AOB=90°,∠AOC=20°,求∠MON的度数.(2)、若∠AOB=x°,∠AOC=y°,则∠MON的大小为 度.(用含x、y的代数式表示)20. 如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?完成下面解答过程中的填空或填写理由.解:∵AB∥CD(已知),
∴∠B= ▲ ( )
∵∠B=∠D=37°(已知)
∴ ▲ =∠D(等量代换)
∴BC∥DE ( ).
 21. 某中学七年级(1)班5名教师决定带领本班x(x>30)名学生去净月潭国家森林公园秋游.该景区现有A、B两种购票方案可供选择:
21. 某中学七年级(1)班5名教师决定带领本班x(x>30)名学生去净月潭国家森林公园秋游.该景区现有A、B两种购票方案可供选择: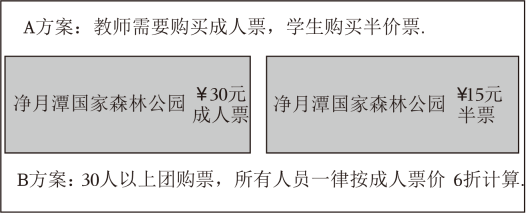 (1)、请用含x的代数式分别表示选择A、B两种方案所需的费用:
(1)、请用含x的代数式分别表示选择A、B两种方案所需的费用:A:元;
B:元.
(2)、当学生人数x=50时,且只选择其中一种方案购票,请通过计算说明选择哪种方案更为优惠.22. 如图,已知点A、B在数轴上分别对应a、b两个数,且|a+4|+(b﹣6)2=0,点O是原点.动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,同时动点Q从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,设运动的时间为t秒. (1)、线段AB的长度为 .(2)、动点P在数轴上对应的数为 . (用含t的代数式表示)(3)、当线段PQ的长度是4时,求t的值.23. 【教材呈现】下图是华师版七年级上册数学教材第117页的部分内容.
(1)、线段AB的长度为 .(2)、动点P在数轴上对应的数为 . (用含t的代数式表示)(3)、当线段PQ的长度是4时,求t的值.23. 【教材呈现】下图是华师版七年级上册数学教材第117页的部分内容.
【阅读理解】
小明通过观察发现:
x2+x+3→2x2+2x﹣3
前后两个多项式中,含x次数相同项的系数存在相同的倍数关系.
思考:只需求得x2+x的值即可求得2x2+2x的值,进而解决问题.
于是他在做作业时采用了如下方法:
由题意,得x2+x+3=7,则有x2+x=4.
2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5.
所以代数式2x2+2x﹣3的值为5.
【方法学习】
这种方法叫整体代入法,是我们在整式求值时常用到的一种方法,即题目已知条件告诉我们的不是单个未知数的值,而是一个或者几个式子的值,让我们根据条件去求其它代数式的值.这个时候,我们要将问题中的式子转化成含有已知式子的形式,然后整体将已知条件代入求值.
(1)、【方法运用】
若代数式x2+2x+2的值为5,求代数式2x2+4x+3的值.(2)、当x=1时,代数式ax3+bx+3的值为9.当x=﹣1时,求代数式ax3+bx+3的值.(3)、【方法拓展】
若2a2﹣3ab=16,2ab﹣b2=﹣12,则代数式2a2﹣5ab+b2的值为 .24. 【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE、DF的反向延长线交于主光轴MN上一点P.
【提出问题】小明提出:∠BPD、∠ABP和∠CDP三个角之间存在着什么样的数量关系?
【分析问题】我们学习过平行线的性质,利用平行线的性质可以把∠BPD分成两部分进行研究.
(1)、【解决问题】请你帮小明解决这个问题,并说明理由.(2)、【举一反三】①如图①,若∠ABE=150°,∠CDF=170°,则∠EPF=度.②如图②,已知AB∥CD,点E、F分别是AB、CD上的点,点P位于AB上方,∠PEB=α,∠PFD=β.用含α和β的代数式表示下列各角.
∠P的大小为 . 如图③,在图②的基础上,若EQ和FQ分别平分∠PEB和∠PFD,则∠Q的大小为 .