吉林省长春市净月高新区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 若式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图, , 直线、与这三条平行线分别交于点、、和点、、 , , , , 则的长是( )
 A、 B、 C、 D、4. 已知关于的一元二次方程的一个解是 , 则方程的另一个解为( )A、 B、 C、 D、5. 如图,某商场有一自动扶梯,其倾斜角为 , 高为米则扶梯的长为( )
A、 B、 C、 D、4. 已知关于的一元二次方程的一个解是 , 则方程的另一个解为( )A、 B、 C、 D、5. 如图,某商场有一自动扶梯,其倾斜角为 , 高为米则扶梯的长为( ) A、米 B、米 C、米 D、米6. 如图,在中, , , 点是边上一动点,连结 , 将沿折叠,当点落在边点时,若 , 则的长是( )
A、米 B、米 C、米 D、米6. 如图,在中, , , 点是边上一动点,连结 , 将沿折叠,当点落在边点时,若 , 则的长是( ) A、 B、 C、 D、7. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若 , , , 为上一动点,则的最小值为( )
A、 B、 C、 D、7. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若 , , , 为上一动点,则的最小值为( )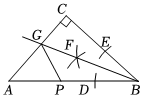 A、 B、 C、 D、8. 如图,在平面直角坐标系中,点、都在反比例函数的图象上,延长交轴于点 , 作轴于点 , 连接、 , 并延长交轴于点若 , 的面积是 , 则的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点、都在反比例函数的图象上,延长交轴于点 , 作轴于点 , 连接、 , 并延长交轴于点若 , 的面积是 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
9. 计算: .10. 关于的一元二次方程有两个不相等实数根,则的取值范围是 .11. 在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 .12. 如图,在平面直角坐标中,与是位似图形,且它们的顶点都在格点上,则位似中心的坐标为 .
 13. 如图,已知点、分别是、边上的点,且∽ , 相似比为: , 交于点 , 则: .
13. 如图,已知点、分别是、边上的点,且∽ , 相似比为: , 交于点 , 则: . 14. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米.
14. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米.
三、计算题:本大题共1小题,共6分。
-
15. 解方程: .
四、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
16. 计算: .17. 在一次试验中,每个电子元件
 的状态有通电、断开两种可能,并且这两种状态的可能性相等.用列表或画树状图的方法,求图中A , B之间电流能够通过的概率.
的状态有通电、断开两种可能,并且这两种状态的可能性相等.用列表或画树状图的方法,求图中A , B之间电流能够通过的概率. 18. 年杭州亚运会吉祥物是由琮琮、莲莲、宸宸共同组成“江南忆”组合三个吉祥物造型形象生动,深受大家的喜爱经统计,某商店月份“江南忆”钥匙扣的销售量为件,月份的销售量为件求该款钥匙扣月份到月份销售量的月平均增长率.
18. 年杭州亚运会吉祥物是由琮琮、莲莲、宸宸共同组成“江南忆”组合三个吉祥物造型形象生动,深受大家的喜爱经统计,某商店月份“江南忆”钥匙扣的销售量为件,月份的销售量为件求该款钥匙扣月份到月份销售量的月平均增长率. 19. 如图,在的正方形网格中,每个小正方形的边长均为 , 的顶点均在格点上,请按下列要求计算并用无刻度的直尺画出图形保留作图痕迹
19. 如图,在的正方形网格中,每个小正方形的边长均为 , 的顶点均在格点上,请按下列要求计算并用无刻度的直尺画出图形保留作图痕迹 (1)、如图 , 在中, ;(2)、如图 , 在边上取一点 , 使得;(3)、如图 , 在边上找一点 , 使得: .20. 如图,在平行四边形中,连接 , 点在边上,连接并延长,交的延长线于点 , 且 .
(1)、如图 , 在中, ;(2)、如图 , 在边上取一点 , 使得;(3)、如图 , 在边上找一点 , 使得: .20. 如图,在平行四边形中,连接 , 点在边上,连接并延长,交的延长线于点 , 且 . (1)、求证:∽;(2)、如果 , , 求的长.21. 在综合与实践活动中,要利用测角仪测量塔的高度如图,塔前有一座高为的观景台 , 已知 , 点、、在同一条水平直线上某学习小组在观景台处测得塔顶部的仰角为 , 在观景台处测得塔顶部的仰角为求塔的高度【参考数据: , 】
(1)、求证:∽;(2)、如果 , , 求的长.21. 在综合与实践活动中,要利用测角仪测量塔的高度如图,塔前有一座高为的观景台 , 已知 , 点、、在同一条水平直线上某学习小组在观景台处测得塔顶部的仰角为 , 在观景台处测得塔顶部的仰角为求塔的高度【参考数据: , 】 22. 【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.
22. 【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.猜想:如图,在中,点、分别是与的中点.
根据画出的图形,可以猜想:
, 且 .
对此,我们可以用演绎推理给出证明.
 (1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 已知矩形中, , , 点在上从向移动,、、分别是、、的中点,则 .(3)、【拓展提升】在平行四边形中, , 点是的中点,过点作平分线的垂线,垂足为点 , 连结 , 若 , 则 .23. 如图,在平行四边形中,为中点, , , 动点从点出发,沿以每秒个单位的速度向终点运动连结 , 过点作 , 且 , 连结 , 点和点始终在直线的同侧设运动的时间为秒
(1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 已知矩形中, , , 点在上从向移动,、、分别是、、的中点,则 .(3)、【拓展提升】在平行四边形中, , 点是的中点,过点作平分线的垂线,垂足为点 , 连结 , 若 , 则 .23. 如图,在平行四边形中,为中点, , , 动点从点出发,沿以每秒个单位的速度向终点运动连结 , 过点作 , 且 , 连结 , 点和点始终在直线的同侧设运动的时间为秒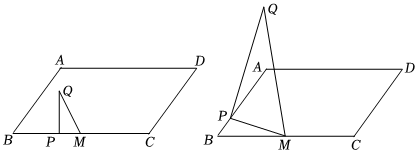 (1)、当点沿运动时,求的长用含的代数式表示 .(2)、当点落在边上时,求的值.(3)、连结 , 当与平行四边形的边平行时,直接写出的值.24. 已知抛物线、、是常数, , 自变量与函数值的部分对应值如表:
(1)、当点沿运动时,求的长用含的代数式表示 .(2)、当点落在边上时,求的值.(3)、连结 , 当与平行四边形的边平行时,直接写出的值.24. 已知抛物线、、是常数, , 自变量与函数值的部分对应值如表: (1)、根据以上信息,可知抛物线开口向 ,对称轴为直线 .(2)、求抛物线的解析式和的值.(3)、将抛物线的图象记为 , 将绕点旋转后的图象记为 , 、合起来得到的图象记为 , 完成以下问题:
(1)、根据以上信息,可知抛物线开口向 ,对称轴为直线 .(2)、求抛物线的解析式和的值.(3)、将抛物线的图象记为 , 将绕点旋转后的图象记为 , 、合起来得到的图象记为 , 完成以下问题:
若直线与函数有且只有两个交点,直接写出的取值范围.
若对于函数上的两点、 , 当 , 时,总有 , 直接写出的取值范围.
-