吉林省白城市大安市2023-2024学年九年级上学期数学期末统考试卷
试卷更新日期：2024-02-01 类型：期末考试
一、选择题（每小题2分，共12分）
-
1. 抛物线y=（x-3）2 +1的对称轴是直线（ ）A、x=3 B、x=-3 C、x=1 D、x=-12. 下列图形中，是中心对称图形的是（ ）A、
B、 
C、
D、
3. 若用配方法解方程x2+8x+7=0，则下列配方正确的是（ ）A、（x-4）2=9 B、（x+4） 2=9 C、（x-8） 2=9 D、（x+8） 2=94. 元旦快到了，已知九年五班同学们要互赠贺卡共420张，设该班共有x名同学，则可列方程为（ ）A、x （x+1） =420 B、（1+x） 2=420 C、x （x-1） =420 D、（1+2x） =4205. 如图，A， B， C是⊙0上的三个点，若∠A0B=58° ，则∠ACB的度数为（ ）
A、58° B、61° C、32° D、29°6. 如图，为抛物线y=ax+bx+c （a≠0） 的部分图象，其对称轴为直线x=1， 与x轴的一个交点坐标为（-1， 0），现有下列判断：①abc>0； ②方程ax2+bx+c=0的两个根是x1=-1， x2=3；③3a+c>0；④当ax2+bx+c>3时， x的取值范围是0＜x＜2；以上结论中正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题（每小题3分，共24分）
-
7. “购买一张彩票，中奖”这一事件是（填“必然事件”“不可能事件”“随机事件”）8. 点P （2a， 2）与Q （-4， 2b）关于原点对称，则a+b=.9. 如图，某地新建一座石拱桥，桥拱是圆弧形，它的跨度AB为60m， 拱高CD为10m， 则桥拱所在圆的半径长为
10. 抛物线y=x2 - 2x + 2的对称轴是直线11. 圆锥的底面直径为80cm，母线长为90cm，则该圆锥侧面展开图的圆心角的度数为12. 如图，将含有30°的直角三角板ABC绕点B按顺时针转动一个角度到A1BC1的位置，使得点A、B、C1在同一条直线上，那么转动的这个角度等于
13. 有6张看上去无差别的卡片，上面分别写着1， 2， 3， 4，5，6，随机抽取1张后，放回并混在一起，再随机抽取1张，则两次取出的数字都是奇数的概率为14. 如图，若抛物线y= ax2 + bx+c上的P（4，0）， Q两点关于它的对称轴直线x= 1对称，则关于x的一元二次方程ax2+ bx+c=0的解是
三、解答题（每小题5分，共20分）
-
15. 解方程： x （x+3） =2 （x+3）16. 第一盒中有1个白球、1个黑球，第二盒中有1个白球，2个黑球．这些球除颜色外无其他差别，分别从每个盒中随机取出1个球，用画树状图或列表的方法，求取出的2个球都是白球的概率．17. 已知：抛物线y=ax2+bx+3经过点A（3， 0）； B（-1. 8）， 求抛物线的函数表达式。18. 图①，图②均是4x4的正方形网格，每个小正方形的顶点称为格点，其中点A， B， C均在格点上，请在给定的网格中按要求画四边形：
(1)、在图①中，找一格点D，使以点A，B，C，D为顶点的四边形是轴对称图形。(2)、在图②中，找-格点E，使以点A，B，C，E为顶点的四边形是中心对称图形。四、解答题（每小题7分，共28分）
-
19. 已知关于x的一元二次方程有实数根。(1)、求m的取值范围；(2)、若两实数根分别为 和 ，且 求 的值.20. 如图，点o是等边△ABC内一点，∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD，
(1)、求证： △COD是等边三角形。(2)、当a= 150°时，OB=4， OC=3，求0A的长。21. 某校数学综合实践小组的同学们去超市调查种国货商品在“双十二”期间的销售情况，下面是调查后同学们之间的交流内容：小泽：该商品的进价为11元/件：
小然：该商品定价为20元时，每天可售出400件；
小远：在定价为20元的基础上，每涨价1元，每天可少售20件。
根据他们调查的内容，若销售的商品每天能获利3800元时，为了尽快减少库存，应该怎样定价更合理？
22. 已知二次函数y=a （x-h）2 ， 当x=4时有最高点，且此函数的图象经过点（1， -3）。(1)、求此二次函数的解析式；(2)、当x为何值时，y随x的增大而减小？五、解答题（每小题8分，共16分）
-
23. 大熊猫属于中国独有的一种动物，数量稀少，被称为“中国国宝”，某店专门销售熊猫公仔玩具，成本为30元/件，每天销售量y （件）与销售单价x （元）之间存在如图所示的一次函数关系。
(1)、求y与x之间的函数关系式；(2)、如果规定每天熊猫公仔玩具的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？24. 如图，AB 为⊙O的直径，点C在00外，∠ABC 的平分线与⊙0交于点D，∠C=90° ，
(1)、CD与⊙O有怎样的位置关系？请说明理由；(2)、若∠CDB=60°，AB=6， 求的长。六、解答题（每小题10分，共20分）
-
25. 有一根长方形直尺宽为4cm，长为10cm，还有一块锐角为45°的直角三角板，它的斜边长为16cm，如图，将直尺的宽DE与直角三角板的斜边AB重合，且点D与点A重合，将直尺沿射线AB方向平移，设平移的长度为xcm，且直尺和三角板重叠部分的面积为Scm2 ，
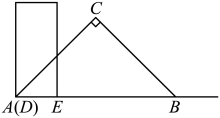(1)、当直角顶点C落在直尺的长上时，x=cm；(2)、当0＜x＜12时，求S与x之间的函数关系式；(3)、是否存在一个位置，使重叠部分面积为28cm2？若存在直接写出x的值，若不存在，请说明理由。26. 如图，抛物线y=x2+bx+c的图象与x轴交于A（-1， 0），B（3，0）两点，与y轴交于点C，
(1)、求抛物线的解析式；(2)、当x为何取值范围时，y随x的增大而增大？(3)、点P是抛物线的对称轴上一动点，若△PBC是直角三角形，求点P的坐标。