吉林省长春市德惠市2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共24分）

1. 5的相反数是（）

A、 $- 5$ B、 $- \frac{1}{5}$ C、 $\frac{1}{5}$ D、5

查看试题解析
2. 2022年我国粮食总产量再创新高，达686530000吨．将数字686530000用科学记数法表示为（　　　）

A、 $0.68653 \times 1 0^{8}$ B、 $6.8653 \times 1 0^{8}$ C、 $6.8653 \times 1 0^{7}$ D、 $68.653 \times 1 0^{7}$

查看试题解析
3. 如图所示，是某个几何体的展开图，该几何体是（）

A、三棱柱 B、三棱锥 C、圆锥 D、圆柱

查看试题解析
4. 如图，利用工具测量角，则 $∠ 1$ 的大小为（）

A、 $30 °$ B、 $60 °$ C、 $120 °$ D、 $150 °$

查看试题解析
5. 如图是小明探索直线平行的条件时所用的学具，木条 $a$ 、 $b$ 、 $c$ 在同一平面内．经测量 $∠ 1 = 70 °$ ，要使木条 $a ∥ b$ ，则 $∠ 2$ 的度数应为（）

A、 $20 °$ B、 $70 °$ C、 $110 °$ D、 $160 °$

查看试题解析
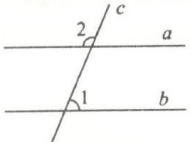6. 如图，体育课上测量跳远成绩的依据是（）

A、平行线间的距离相等 B、两点之间，线段最短 C、垂线段最短 D、两点确定一条直线

查看试题解析
7. 将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（）

A、140° B、160° C、170° D、150°

查看试题解析
8. 在 $| (- 5) + □ |$ 的“□”中填入一个数，使结果等于11，这个数是（）

A、 $- 6$ B、16 C、 $- 6$ 或16 D、6或 $- 16$

查看试题解析

二、填空题（每小题3分，共18分）

9. 计算： ${(\frac{- 2 x^{2}}{y})}^{3}$ ＝．

查看试题解析
10. 已知 $∠ α = 37 ° 4 5^{'}$ ，则 $∠ α$ 的余角等于．

查看试题解析
11. 如图，甲从点 $A$ 出发向北偏东 $60 °$ 方向走到点 $B$ ，乙从点 $A$ 出发走到点 $C$ ，若 $∠ B A C = 140 °$ ，则乙从点 $A$ 出发沿方向走到点 $C$ ．

查看试题解析
12. 如图，直线 $A B$ 与 $C D$ 交于点O ， $O E$ 平分 $∠ A O D$ ，若 $∠ A O C = 44 °$ ，则 $∠ D O E$ 的度数为．

查看试题解析
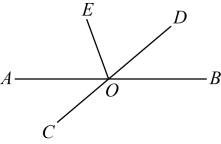13. 为了帮助地震灾区重建家园，某班全体师生积极捐款，捐款金额共3150元，其中5名教师人均捐款a元，则该班学生共捐款元（用含有a的代数式表示）．

查看试题解析
14. 如图是路灯维护工程车的工作示意图，工作篮底部与支撑平台平行．若 $∠ 1 = 30 °$ ，则 $∠ 2 + ∠ 3$ 的度数为．

查看试题解析

三、解答题（共78分）

15.

(1)、计算： $3 \div (- \frac{1}{2}) - (\frac{2}{5} - \frac{1}{3}) \times 15$

(2)、计算： $(- 3)^{2} - (- 2)^{3} \times (- \frac{1}{4}) - (- 1 + 6)$

查看试题解析
16. 化简求值： $4 (a^{2} b + a b^{2}) - 3 (a^{2} b - 1) + 2 a b^{2} - 6$ ，其中 $a = 1$ ， $b = - 4$ ．

查看试题解析
17. 如图，在一条不完整的数轴上从左到右有点 $A$ 、 $B$ 、 $C$ 、 $D$ ，其中 $A D = 6$ ，且 $A B = B C = C D$ ．

(1)、则 $B C$ 的长为；

(2)、若点 $C$ 对应的数是2，点 $A$ 、 $B$ 、 $D$ 所对应的数分别为 $a$ 、 $b$ 、 $d$ ，求 $| a + b + d |$ 的值．

查看试题解析
18. 数学活动课上，小明设计如下五张卡片并提出了如下问题，请同学们完成小明提出的问题：
将卡片上的数化简后写在横线上，并画数轴，将横线上的结果在数轴上表示出来．

-（+3.5）


（-1）7


-0.5的倒数


+|-2.5|

比-1大 $\frac{5}{2}$ 的数

（1）（2）（3）（4）（5）

查看试题解析
19. 如图是由6个棱长都为1的小正方体搭成的几何体．
左视图俯视图

(1)、请在下面方格纸中分别画出它的左视图和俯视图；

(2)、如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的左视图和俯视图不变，那么最多可以添加个小正方体．

查看试题解析
20. 如图，点B为线段 $A D$ 的中点，点C在线段 $B D$ 上，且 $C D = 2 B C$ ，若 $B C = 3$ ，求 $A D$ 的长．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ 交线段 $B C$ 于点 $E$ ， $∠ 1 = ∠ 2$ ， $∠ A = 100 °$ ．求 $∠ B$ 的度数．

查看试题解析
22. 【阅读理解】“整体思想”是一种重要的数学思想方法，在多项式的化简求值中应用极为广泛．
例如： $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a - b)$ 看成一个整体，则 $4 (a - b) - 2 (a - b) + (a - b) = (4 - 2 + 1) (a - b) = 3 (a - b)$ ．
【尝试应用】根据阅读内容，运用“整体思想”，解答下列问题：

(1)、化简 $8 (a + b) + 6 (a + b) - 2 (a + b)$ 的结果是．

(2)、化简求值： $9 {(x + y)}^{2} + 3 (x + y) + 7 {(x + y)}^{2} - 7 (x + y)$ ，其 $(x + y) = \frac{1}{2}$ ．

(3)、【拓展探索】
若 $x^{2} - 2 y = 4$ ，求代数式 $- 3 x^{2} + 6 y + 2$ 的值．

查看试题解析
23. 习近平总书记强调：“加强学校体育工作，推动青少年文化学习和体育锻炼协调发展，帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锻炼意志”．体育是教育的重要组成部分，其功能既包括锻炼身体、增强体质，也包括塑造品格、养成精神、某校为积极响应国家的号召，决定添置一批体育器材．学校准备在网上订购一批某品牌足球和跳绳，在查阅天猫网店后发现足球每个定价140元，跳绳每条定价30元．现有 $A$ 、 $B$ 两家网店均提供包邮服务，并提出了各自的优惠方案． $A$ 网店：买一个足球送一条跳绳； $B$ 网店：足球和跳绳都按定价的90%付款．已知要购买足球60个，跳绳 $x$ 条 $(x > 60)$ ．

(1)、若在 $A$ 网店购买，需付款元，若在 $B$ 网店购买，需付款元（用含 $x$ 的代数式表示，结果需要化简）；

(2)、当 $x = 200$ 时，通过计算说明此时在 $A$ 、 $B$ 哪一家网店购买较为合算?

(3)、当 $x = 200$ 时，设计一种更为省钱的购买方案，并计算需付款多少元?

查看试题解析
24. 已知 $A B ∥ C D$ ，点 $E$ 在 $A B$ 上，点 $F$ 在 $D C$ 上，点 $G$ 为射线 $E F$ 上一点．

(1)、【基础问题】如图1，试说明： $∠ A G D = ∠ A + ∠ D$ ．（完成下面的填空部分）
证明：过点 $G$ 作直线 $M N ∥ A B$ ，
$∵ A B ∥ C D$ ，
$∴$     ①    ▲   $∥ C D$ ．
$∵ M N ∥ A B$ ，
$∴$     ②▲ $= ∠ M G A$ ．
$∵ M N ∥ C D$ ，
$∴ ∠ D =$     ③    ▲     （    ④▲  ）．
$∴ ∠ A G D = ∠ A G M + ∠ A G M = ∠ A + ∠ D$ ．

(2)、【类比探究】如图2，当点 $G$ 在线段 $E F$ 延长线上时，请写出 $∠ A G D$ 、 $∠ A$ 、 $∠ D$ 三者之间的数量关系，并说明理由．

(3)、【应用拓展】如图3，点 $E$ 与点 $A$ 重合， $A H$ 平分 $∠ G A B$ ，且 $∠ H D F = 22 °$ ， $∠ A F C = 72 °$ ，那么 $∠ H$ 的度数为．

查看试题解析

-（+3.5）	（-1）7	-0.5的倒数	+\|-2.5\|	比-1大 $\frac{5}{2}$ 的数
（1）	（2）	（3）	（4）	（5）