吉林省长春市汽开区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的值为( )A、 B、 C、 D、2. 将二次函数化成的形式为( )A、 B、 C、 D、3. 若点在二次函数图象的对称轴上,则点的坐标可能是( )A、 B、 C、 D、4. 某学校每年抽出一部分资金购买书籍用于扩充图书室已知年该学校用于购买图书的费用为元,年用于购买图书的费用增加到元设该校这两年购买图书的费用的年平均增长率为 , 根据题意可列方程为( )A、 B、 C、 D、5. 已知点是外一点,且的半径为 , 则的长可能为( )A、 B、 C、 D、6. 如图,某零件的外径为 , 用一个交叉卡钳可测量零件的内孔直径若:: , 且量得 , 则零件的厚度为( )
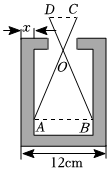 A、 B、 C、 D、7. 如图,一架梯子斜靠在墙上,梯子的长为米,梯子与地面形成的夹角为 , 则墙的高度为( )
A、 B、 C、 D、7. 如图,一架梯子斜靠在墙上,梯子的长为米,梯子与地面形成的夹角为 , 则墙的高度为( )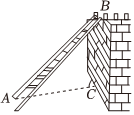 A、米 B、米 C、米 D、米8. 如图,在圆形纸板上裁剪两个扇面具体操作如下:作的任意一条直径 , 以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、 , 得到两个扇形,并裁剪下来若的半径为 , 则剩余纸板图中阴影部分图形的面积为( )
A、米 B、米 C、米 D、米8. 如图,在圆形纸板上裁剪两个扇面具体操作如下:作的任意一条直径 , 以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、 , 得到两个扇形,并裁剪下来若的半径为 , 则剩余纸板图中阴影部分图形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
9. 关于x的方程x2-2x+k=0有两个相等的实数根,则k的值是 .10. 抛物线的顶点坐标为 .11. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点、、都在横格线上若线段 , 则线段 .
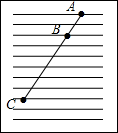 12. 如图,是的切线,是切点,连结、若 , 则的大小为 度
12. 如图,是的切线,是切点,连结、若 , 则的大小为 度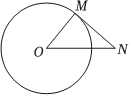 13. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q. 若AB=4,则弧BQ的长为.
13. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q. 若AB=4,则弧BQ的长为. 14. 跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为一条抛物线如图是小冬与小雪将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为米,并且相距米,现以两人的站立点所在的直线为轴,建立如图所示的平面直角坐标系,其中小冬拿绳子的手的坐标是身高米的小丽站在绳子的正下方,且距轴米时,绳子刚好经过她的头顶若身高米的小伟站在这条绳子的正下方,他距轴米,为确保绳子超过他的头顶,则的取值范围为 .
14. 跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为一条抛物线如图是小冬与小雪将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为米,并且相距米,现以两人的站立点所在的直线为轴,建立如图所示的平面直角坐标系,其中小冬拿绳子的手的坐标是身高米的小丽站在绳子的正下方,且距轴米时,绳子刚好经过她的头顶若身高米的小伟站在这条绳子的正下方,他距轴米,为确保绳子超过他的头顶,则的取值范围为 .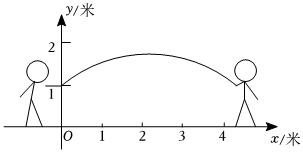
三、计算题:本大题共1小题,共6分。
-
15. 解方程:x2-4x+1=0
四、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
16. 现有三张不透明的卡片,其中两张卡片的正面图案均为成都第届世界大学生夏季运动会会徽卡片分别记为 , , 第三张卡片的正面图案为成都第届世界大学生夏季运动会吉祥物“蓉宝”卡片记为 , 卡片除正面图案不同外,其余均相同将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张请用画树状图或列表的方法,求两次抽出的卡片上的图案都是“蓉宝”的概率.
 17. 已知二次函数的图象经过点、 , 求这个二次函数的表达式.18. 在汽开区中小学科技节会场上,一架无人机进行实时航拍如图,无人机在空中处的飞行高度为 , 地面观测点处观测无人机在空中处的仰角 , 已知米,求此时无人机的飞行高度结果精确到米
17. 已知二次函数的图象经过点、 , 求这个二次函数的表达式.18. 在汽开区中小学科技节会场上,一架无人机进行实时航拍如图,无人机在空中处的飞行高度为 , 地面观测点处观测无人机在空中处的仰角 , 已知米,求此时无人机的飞行高度结果精确到米
【参考数据: , , 】 19. 图、图、图均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上,点为的中点只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
19. 图、图、图均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上,点为的中点只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.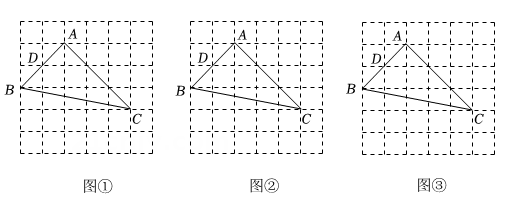 (1)、在图中的边上确定一点 , 连结 , 使 .
(1)、在图中的边上确定一点 , 连结 , 使 .
(2)、在图中的边上确定一点 , 连结 , 使 .
(3)、在图中的边上确定一点 , 连结 , 使 .20. 如图,为的直径,点、都在上,且平分 , 过点作 , 交的延长线于点 .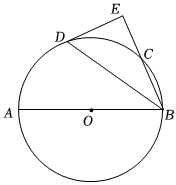 (1)、求证:是的切线.
(1)、求证:是的切线.
(2)、延长交的延长线于点若 , , 则的长为 .21. 如图,在平面直角坐标系中,抛物线经过点和点 , 顶点为 .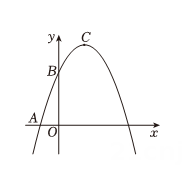 (1)、求这条抛物线所对应的二次函数的表达式.
(1)、求这条抛物线所对应的二次函数的表达式.
(2)、求顶点的坐标.
(3)、当时,直接写出的取值范围.22. 【问题呈现】小华在一次学习过程中遇到了下面的问题: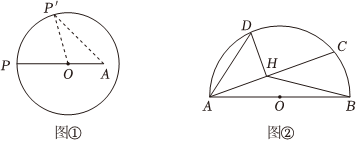
点为内一定点,点为上一动点,确定点的位置,使线段最长.(1)、【问题解决】以下是小华的方法:
如图 , 连结并延长交于点 , 点为所求.
理由如下:在上取点异于点 , 连结、 .
接下来只需证明 .
请你补全小华的证明过程.
(2)、【类比结论】点为外一定点,点为上一动点,设的半径为 , 的长为 , 则线段长度的最大值为 ,线段长度的最小值为 用含、的代数式表示
(3)、【拓展延伸】如图 , 在半圆中,直径的长为 , 点在半圆上, , 点在上运动,连结 , 是上一点,且 , 连结在点运动的过程中,线段长度的最小值为 .23. 如图,在中, , , , 点为边的中点,动点从点出发,沿折线向点运动,点在上以每秒个单位长度的速度运动,在上以每秒个单位长度的速度运动,在点运动过程中,连结 , 将沿翻折得到设点的运动时间为秒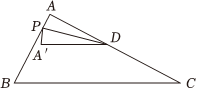 (1)、求的长.
(1)、求的长.
(2)、用含的代数式表示线段的长.
(3)、当与相似时,求的值.
(4)、当四边形为中心对称图形时,直接写出的值.24. 在平面直角坐标系中,抛物线经过点点是该抛物线上一点,其横坐标为以为对角线作矩形 , 轴.(1)、求抛物线所对应的函数表达式.
(2)、当抛物线在矩形内部的点的纵坐标随的增大而减小时,的取值范围为 .
(3)、设抛物线在矩形内部的图象包括边界的最高点的纵坐标与最低点的纵坐标之差为时,求与之间的函数关系式.
(4)、设这条抛物线的顶点为 , 的面积为当时,直接写出的值.
-