吉林省重点学校2023-2024学年七年级上学期数学期末考试试卷(五四学制)
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列分别表示“节水”、“节能”、“回收”、“绿色食品”含义的四个标志的图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中,解为的是( )A、 B、 C、 D、3. 若 , 则下列式子中,不正确的是( )A、 B、 C、 D、4. 某人用同种正多边形瓷砖铺设无缝地板,他购瓷砖形状可能是( )A、正五角形 B、正六边形 C、正七边形 D、正九边形5. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm6. 孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短引绳度之,余绳四尺五寸:屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余尺:将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是( )A、 B、 C、 D、7. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、
2. 下列方程中,解为的是( )A、 B、 C、 D、3. 若 , 则下列式子中,不正确的是( )A、 B、 C、 D、4. 某人用同种正多边形瓷砖铺设无缝地板,他购瓷砖形状可能是( )A、正五角形 B、正六边形 C、正七边形 D、正九边形5. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm6. 孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短引绳度之,余绳四尺五寸:屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余尺:将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是( )A、 B、 C、 D、7. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、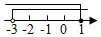 B、
B、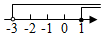 C、
C、 D、
D、 8. 如图,沿着点到点的方向平移到的位置, , , , 平移距离为 , 则阴影部分的面积为( )
8. 如图,沿着点到点的方向平移到的位置, , , , 平移距离为 , 则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
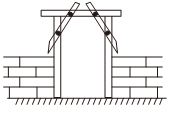
9. 已知是方程的解,则的值为 .10. 如图,木工师傅做长方形门框时,会在门上斜着钉两条木板,使其不变形,这样做的数学原理是 .
 11. 某正六边形的雪花图案如图所示这个图案绕着它的中心旋转一定角度后能与自身重合,则这个旋转角的大小至少为 度
11. 某正六边形的雪花图案如图所示这个图案绕着它的中心旋转一定角度后能与自身重合,则这个旋转角的大小至少为 度 12. 一个多边形的每个内角都是 , 则这个多边形是 边形.13. 若关于的方程是一元一次方程,则这个方程的解14. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
12. 一个多边形的每个内角都是 , 则这个多边形是 边形.13. 若关于的方程是一元一次方程,则这个方程的解14. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
-
15. 解下列方程或不等式 .(1)、;
(2)、 .16. 解不等式组,并将其解集在数轴表示出来.
.17. 下面是小张同学解二元一次方程组的过程,请认真阅读并回答相应的问题.解方程组:
解: , 得第一步
, 得第二步
第三步
代入 , 得第四步
所以,原方程组的解为第五步(1)、小彬同学的解题过程从第 步开始出现错误;(2)、请写出正确的解题过程;(3)、解二元一次方程组的基本思想是“消元”,即把“二元”变为“一元”,在此过程中体现的数学思想是 填序号 .
.数形结合
.类比思想
.转化思想
.分类讨论18. 已知一个多边形的内角和比外角和多720°,求这个多边形的每个内角度数与边数n .19. 如图,在中,平分交于点 , 平分交于点 , 若 , 求的度数. 20. 已知、、为的三边长,且、满足 , 为方程的解,求的周长.21. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?22. 如图,在的方格纸巾有一条直线和 , 请按要求解答.
20. 已知、、为的三边长,且、满足 , 为方程的解,求的周长.21. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?22. 如图,在的方格纸巾有一条直线和 , 请按要求解答.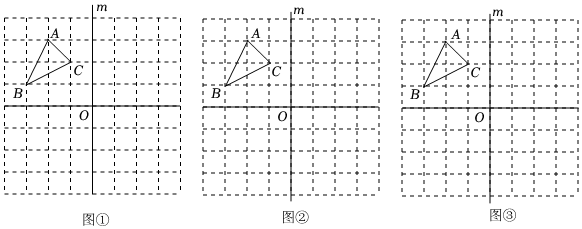 (1)、将向右平移个单位,在图中画出平移后的;(2)、在图中画出关于直线对称的;(3)、将绕点旋转 , 在图中画出旋转后的 .23. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、 .
(1)、将向右平移个单位,在图中画出平移后的;(2)、在图中画出关于直线对称的;(3)、将绕点旋转 , 在图中画出旋转后的 .23. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、 . (1)、如图 , 若时,点在内,则 度, 度, 度;(2)、如图 , 改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.(3)、如图 , 改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.24. 如图,在长方形中, , 点从点出发,沿折线以每秒个单位的速度向点运动,同时点从点出发,沿以每秒个单位的速度向点运动,当点到达点时,点、同时停止运动设点的运动时间为秒.
(1)、如图 , 若时,点在内,则 度, 度, 度;(2)、如图 , 改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.(3)、如图 , 改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.24. 如图,在长方形中, , 点从点出发,沿折线以每秒个单位的速度向点运动,同时点从点出发,沿以每秒个单位的速度向点运动,当点到达点时,点、同时停止运动设点的运动时间为秒.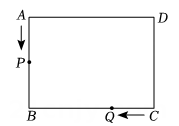 (1)、当点在边上运动时, ;当点在边上运动时, 用含的代数式表示(2)、当点与点重合时,求的值.(3)、当时,求的面积.(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.
(1)、当点在边上运动时, ;当点在边上运动时, 用含的代数式表示(2)、当点与点重合时,求的值.(3)、当时,求的面积.(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.