吉林省长春市南关区2023-2024学年七年级上学期期末数学考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的相反数是( )A、 B、 C、 D、2. 随着科学技术的不断提高,网络已经成为新时代的“宠儿”,预计到年,全球用户将达到人将用科学记数法表示为( )A、 B、 C、 D、3. 下列单项式中,与是同类项的是( )A、 B、 C、 D、4. 下列去括号正确的是( )A、 B、 C、 D、5. 如所示四个图形中,不能作为正方体的展开图的是( )A、
 B、
B、 C、
C、 D、
D、 6. 将多项式按的升幂排列的结果是( )A、 B、 C、 D、7. 如图,从地到地有三条路线,由上至下依次记为、、 , 则从地到地的最短路径是 , 其中蕴含的数学道理是( )
6. 将多项式按的升幂排列的结果是( )A、 B、 C、 D、7. 如图,从地到地有三条路线,由上至下依次记为、、 , 则从地到地的最短路径是 , 其中蕴含的数学道理是( ) A、直线比曲线短 B、两点确定一条直线
A、直线比曲线短 B、两点确定一条直线
C、两点之间,线段最短 D、经过一点有无数条直线8. 如图,点 , 在直线上,点 , 在直线上, , , , 点到直线的距离是( ) A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度9. 一副三角尺按如图所示位置放置,为公共边,量角器中心与点重合,为刻度线如果三角尺一边与刻度线重合,那么边与下列刻度线重合的是( )
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度9. 一副三角尺按如图所示位置放置,为公共边,量角器中心与点重合,为刻度线如果三角尺一边与刻度线重合,那么边与下列刻度线重合的是( ) A、刻度线 B、刻度线 C、刻度线 D、刻度线10. 如图,把两张大小相同的长方形卡片如图按图、图两种方式放在一个底面为长方形长比宽大的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图中阴影部分的周长为 , 图中阴影部分的周长为 , 那么比大( )
A、刻度线 B、刻度线 C、刻度线 D、刻度线10. 如图,把两张大小相同的长方形卡片如图按图、图两种方式放在一个底面为长方形长比宽大的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图中阴影部分的周长为 , 图中阴影部分的周长为 , 那么比大( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
11. 比较大小; 填“”、“=”或“”12. 计算: .13. 某种商品千克的售价为元,那么这种商品千克的售价为 元14. 如图, , 直线经过点 , , , 则 .
 15. 已知线段 , 点在直线上,且 , 若是的中点,则的长为 .16. 观察所示图形:它们是按一定规律排列的,依此规律,第个图形中的共有 个
15. 已知线段 , 点在直线上,且 , 若是的中点,则的长为 .16. 观察所示图形:它们是按一定规律排列的,依此规律,第个图形中的共有 个
三、解答题:本题共12小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算: .18. 计算:19. 计算:20. 计算: .21. 先化简,再求值: , 其中 , .22. 如图,是的正方形网格,每个小正方形的顶点为格点,线段的两个端点及点均在格点上.
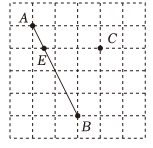 (1)、过点作的垂线,垂足为点;(2)、过点作的平行线点、在点的异侧,点在点上方;(3)、是线段与网格线的交点,连接、 .
(1)、过点作的垂线,垂足为点;(2)、过点作的平行线点、在点的异侧,点在点上方;(3)、是线段与网格线的交点,连接、 .
写出的同旁内角 ;
写出与相等的角 ;
比较线段的大小: , 填“”、“”或“”23. 如图,直线、相交于点 , 平分 , 若 , 求的度数. 24. 如图是长春市南北方向上地铁一号线的线路图,途中共设个站点某天,李华参加该线路上的志愿者服务活动,从北环城路站出发,最后在站结束服务活动如果规定向南为正,向北为负,李华当天乘坐地铁的站数按先后顺序依次记录如下单位:站: , , , , , , , , .
24. 如图是长春市南北方向上地铁一号线的线路图,途中共设个站点某天,李华参加该线路上的志愿者服务活动,从北环城路站出发,最后在站结束服务活动如果规定向南为正,向北为负,李华当天乘坐地铁的站数按先后顺序依次记录如下单位:站: , , , , , , , , . (1)、请通过计算说明站是哪一站?
(1)、请通过计算说明站是哪一站?
(2)、若相邻两站之间的平均距离约为千米,求这次李华志愿服务期间乘坐地铁行进的总路程约是多少千米?25. 如图,已知 , , , 求证: .
阅读下面的解答过程,填空并填写理由.
证明:
已知 ,
▲
已知 ,
等量代换 .
▲
▲
又已知 ,
.
.26. 某学校为了全面提高学生的综合素养,开展了音乐、朗诵、舞蹈、美术共四个社团,学生积极参加每个学生限报一项 , 参加社团的学生共有人,其中音乐社团有人参加,朗诵社团的人数比音乐社团人数的一半多人,舞蹈社团的人数比朗诵社团人数的倍少人.(1)、参加朗诵社团有 人,参加舞蹈社团有 人用含 , 的式子表示
(2)、求美术社团有多少人?用含 , 的式子表示
(3)、若 , , 求美术杜团的人数.27. (1)、【猜想】如图 , , 点在直线、之间,连结、若 , , 则的大小为 度
(1)、【猜想】如图 , , 点在直线、之间,连结、若 , , 则的大小为 度
(2)、【探究】如图 , 、、交于点 , 探究、、之间的数量关系.
(3)、【拓展】如图 , , 、分别平分和 , 且、所在直线交于点 , 过点作 , 若 , 则 度28. 如图,点、、、由左至右依次均在数轴上,点在原点, , , , 点从点出发,沿方向以的速度运动,同时点从点出发沿方向向点匀速运动点运动到点时停止运动 , 设运动的时间为秒. (1)、点表示的数是 ,点表示的数是 点用含的代数式表示(2)、点在线段上,当时,点运动到的位置恰好是线段的中点,求点的运动速度.(3)、若点的运动速度为 , 经过多长时间、两点相距?
(1)、点表示的数是 ,点表示的数是 点用含的代数式表示(2)、点在线段上,当时,点运动到的位置恰好是线段的中点,求点的运动速度.(3)、若点的运动速度为 , 经过多长时间、两点相距?