吉林省吉林市桦甸市2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 点P(-2,5)关于x轴对称的点的坐标为( )A、(2,-5) B、(5,-2) C、(-2,-5) D、(2,5)3. 在一些美术字中,有的汉字是轴对称图形.下面个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图, , 分别是 , 边上的点, , 若添加下列一个条件后,仍不能证明≌的是( )
4. 如图, , 分别是 , 边上的点, , 若添加下列一个条件后,仍不能证明≌的是( )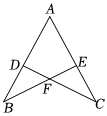 A、 B、 C、 D、5. 若分式的值为 , 则的值为( )A、 B、 C、或 D、或6. 关于的方程的解为正数,则的取值范围是( )A、 B、 C、且 D、且
A、 B、 C、 D、5. 若分式的值为 , 则的值为( )A、 B、 C、或 D、或6. 关于的方程的解为正数,则的取值范围是( )A、 B、 C、且 D、且二、填空题:本题共8小题,每小题3分,共24分。
-
7. 如果一个多边形的内角和是外角和的2倍,则这个多边形是边形.8. “燕山雪花大如席,片片吹落轩辕台”这是诗仙李白眼里的雪花单个雪花的重量其实很轻,只有左右,用科学记数法可表示为 .9. 已知等腰三角形的两边长分别是4和9,则周长是 .10.
空调安装在墙上时,一般都会象如图所示的方法固定在墙上,这种方法应用的数学知识是 .
 11. 已知 , , 则的值为 .12. 如图,在中, , , , 则的长为 .
11. 已知 , , 则的值为 .12. 如图,在中, , , , 则的长为 . 13. 若 , 则 .14. 如图,在 中,点D、E分别是边BC、AB的中点.若 的面积等于8,则 的面积等于 .
13. 若 , 则 .14. 如图,在 中,点D、E分别是边BC、AB的中点.若 的面积等于8,则 的面积等于 .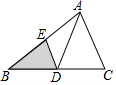
三、解答题:本题共12小题,共84分。解答应写出文字说明,证明过程或演算步骤。
-
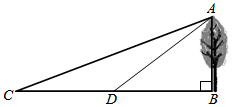
15. 化简: .16. 因式分解: .17. 解方程: .18. 如图,树垂直于地面,为测树高,小华在处测得 , 然后他沿方向走了米,到达处,测得 , 你能帮助小华计算出树的高度吗?
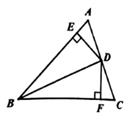
 19. 先化简,再求值: , 其中 , .20. 已知:在△ABC中,DE⊥AB,DF⊥BC,垂足分别为点E,F,且∠ADE=∠CDF,AD=CD,连接BD。
19. 先化简,再求值: , 其中 , .20. 已知:在△ABC中,DE⊥AB,DF⊥BC,垂足分别为点E,F,且∠ADE=∠CDF,AD=CD,连接BD。求证:BD平分∠ABC。
 21. 如图,在平面直角坐标系中,顶点的坐标分别是、、 .
21. 如图,在平面直角坐标系中,顶点的坐标分别是、、 . (1)、画出关于轴对称的 , 并写出各顶点的坐标;(2)、求出的面积.22. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .
(1)、画出关于轴对称的 , 并写出各顶点的坐标;(2)、求出的面积.22. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .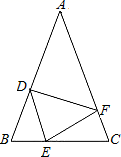 (1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.23.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.23.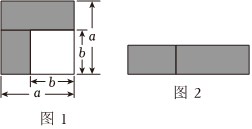
探究活动:
(1)、如图是边长分别为、的正方形,可以求出阴影部分的面积是 写成两数平方差的形式(2)、如图 , 若将图中阴影部分裁剪下来,重新拼成一个长方形,面积是 写成多项式乘积的形式
(3)、比较图、图阴影部分的面积,可以得到等式: .(4)、计算:
计算 .24. 李师傅近期准备换车,看中了价格相同的两款国产车.燃油车
油箱容积:升
油价:元升
续航里程:千米
每千米行驶费用:元新能源车
电池电量:千瓦时
电价:元千瓦时
续航里程:千米
每千米行驶费用: ▲ 元(1)、用含的代数式表示出新能源车每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车每千米行驶费用多元请你帮李师傅计算一下,这两款车的每千米行驶费用各是多少?25. 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.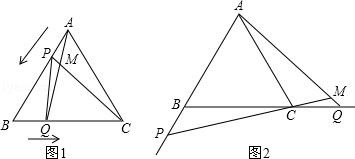 (1)、求证:△ABQ≌△CAP;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.26. 为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小红在组内做了如下尝试:如图 , 在中,是边上的中线,延长到 , 使 , 连接 .
(1)、求证:△ABQ≌△CAP;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.26. 为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小红在组内做了如下尝试:如图 , 在中,是边上的中线,延长到 , 使 , 连接 .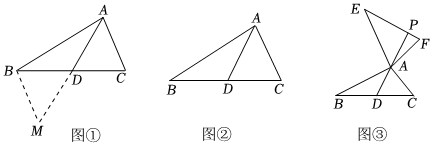 (1)、如图 , 与的数量关系是 ,位置关系是 ;(2)、【初步应用】如图 , 中,若 , , 求边上中线的取值范围;(3)、【探究提升】如图 , 是的边中线,过点分别向外作、 , 使得 , , 延长交于点 , 判断线段与的数量关系和位置关系,并说明理由.
(1)、如图 , 与的数量关系是 ,位置关系是 ;(2)、【初步应用】如图 , 中,若 , , 求边上中线的取值范围;(3)、【探究提升】如图 , 是的边中线,过点分别向外作、 , 使得 , , 延长交于点 , 判断线段与的数量关系和位置关系,并说明理由.