吉林省松原市宁江区2023-2024学年八年级上学期数学期末考试试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 跨学科红细胞系统分为原始红细胞、早幼红细胞、中幼红细胞、晚幼红细胞、网织红细胞和成熟红细胞．某原始红细胞胞体直径为0.000015m，呈圆形或椭圆形，边缘常有钝角状或瘤状突起．将0.000015用科学记数法表示为（）

A、 $1.5 \times 1 0^{- 5}$ B、 $15 \times 1 0^{- 6}$ C、 $0.15 \times 1 0^{- 4}$ D、 $1.5 \times 1 0^{5}$

查看试题解析
2. 化简 $m^{2} \cdot {(- m)}^{3}$ 的结果是（）

A、 $m^{5}$ B、 $- m^{3}$ C、 $m^{6}$ D、 $- m^{6}$

查看试题解析
3. 如图，在△ABC中，AB=15，BC=9，BD是AC边上的中线，若△ABD的周长为30，则△BCD的周长是（）

A、20 B、24 C、26 D、28

查看试题解析
4. 如图，AD是等边 $△ A B C$ 的一条中线，若在边AC上取一点E ，使得 $A E = A D$ ，则 $∠ E D C$ 的度数为（）

A、30° B、20° C、25° D、15°

查看试题解析
5. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于D ， $B E ⊥ A C$ 于E ， AD交EF于F ，若 $B F = A C$ ，则 $∠ A B C$ 等于（）

A、45° B、48° C、50° D、60°

查看试题解析
6. 数学文化《九章算术》中记录的一道题译为白话文是：把一份文件用慢马送到900里外的城市，需要的时间比规定时间多1天；如果用快马送，所需的时间比规定时间少3天，已知快马的速度是慢马的2倍，求规定时间．设规定时间为x天，则可列方程为（）

A、 $\frac{900}{x + 1} \times 2 = \frac{900}{x - 3}$ B、 $\frac{900}{x + 1} = \frac{900}{x - 3} \times 2$ C、 $\frac{900}{x - 1} \times 2 = \frac{900}{x + 3}$ D、 $\frac{900}{x - 1} = \frac{900}{x + 3} \times 2$

查看试题解析

二、填空题（每小题3分，共24分）

7. 已知 ${(x - 3)}^{2} = x^{2} + 2 m x + 9$ ，则m的值是．

查看试题解析
8. 如图， $A C = A D$ ，要使 $△ A C B ≌ △ A D B$ ，还需添加一个条件，这个条件可以是．（写出一个即可）

查看试题解析
9. 化简 $\frac{x^{2}}{x - 1} - \frac{x}{x - 1}$ 的值为．

查看试题解析
10. 如图，在 $△ A B C$ 中，DE是AC的垂直平分线，若 $A E = 3$ cm， $△ A B D$ 的周长是13cm，则 $△ A B C$ 的周长为cm．

查看试题解析
11. 若 $3 x + 2 y - 3 = 0$ ，则 $8^{x} \cdot 4^{y} =$ ．

查看试题解析
12. 真实情境：小明将两把完全相同的长方形直尺按如图放置在 $∠ A O B$ 上，两把直尺的接触点为点P ，边OA与其中一把直尺边缘的交点为C ，点C ， P在这把直尺上的刻度读数分别是2，5，则OC的长度是cm．

查看试题解析
13. 定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”．若等腰 $△ A B C$ 是“倍长三角形”，底边BC长为5，则等腰 $△ A B C$ 的周长为．

查看试题解析
14. 对于两个不相等的实数a、b ，我们规定符号 $M i n {a ， b}$ 表示a ， b中的较小的值，如 $M i n {2 ， 4} = 2$ ，按照这个规定，方程 $M i n (\frac{1}{1 - x} ， \frac{2}{1 - x}) = \frac{4}{x - 1} - 3$ 的解为．

查看试题解析

三、解答题（每小题5分，共20分）

15. 分解因式： $x^{2} (m - n) + 9 (n - m)$ ．

查看试题解析
16. 解方程： $\frac{15}{x} = \frac{24}{x + 3}$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D在AC上，且 $B D = B C = A D$ ，求 $∠ A B D$ 的度数．

查看试题解析
18. 如图，已知 $∠ A = ∠ D = 90 °$ ， $A C = B D$ ．求证： $A B = C D$ ．

查看试题解析

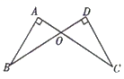
四、解答题（每小题7分，共28分）

19. 先化简，再求值： $(1 - \frac{2}{x - 1}) \cdot \frac{x^{2} - x}{x^{2} - 6 x + 9}$ ，其中 $x = 13$ ．

查看试题解析
20. 如图，在 $△ A B C$ 中，点M ， N分别是AB和AC上的点， $M N ∥ B C$ ，且 $B C = 2 M N$ ，点E是CN的中点，连接ME并延长交BC的延长线于点D ．若 $C D = 4$ ，求BC的长．

查看试题解析
21. 跨学科习近平总书记指出，中华优秀传统文化是中华民族的“根”和“魂”，是最深厚的文化软实力，是中国特色社会主义植根的沃土，是我们在世界文化激荡中站稳脚跟的根基．为了大力弘扬中华优秀传统文化，某校决定开展名著读书活动，用3600元购买“四大名著”若干套后，发现这批图书满足不了学生的阅读需求，图书管理员在购买第二批时正赶上图书城8折销售该套书，于是用2400元购买的套数只比第一批少4套。

(1)、求第一批购进的“四大名著”每套的价格是多少元；

(2)、该校共购进“四大名著”多少套？

查看试题解析
22. 如图，有两个 $7 \times 4$ 的网格，网格中每个小正方形的边长均为1，每个网格中各画有一个梯形．请在图1，图2中分别画出一条线段，同时满足以下要求：
$(1)$ 线段的一个端点为梯形的顶点，另一个端点在梯形一边的格点上；
$(2)$ 将梯形分成两个图形，其中一个是轴对称图形；
$(3)$ 图1，图2中分成的轴对称图形不全等．

查看试题解析

五、解答题（每小题8分，共16分）

23. 如图，在△ABC中，AB＝AC，点D在BC边上，点E在AC边上，连接AD、DE，若AD=DE，AC＝CD．

(1)、求证：△ABD≌△DCE；

(2)、若BD＝3，CD＝5，求AE的长．

查看试题解析
24. 观察下列等式，回答问题．
$(x - 1) (x + 1) = x^{2} - 1$ ；
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；
$(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1$ ；

(1)、试求 $2^{6} + 2^{5} + 2^{4} + 2^{3} + 2^{2} + 2 + 1$ 的值；

(2)、判断 $2^{2008} + 2^{2007} + 2^{2006} + \cdot \cdot \cdot + 2^{2} + 2 + 1$ 的值的个位数字是几？

查看试题解析

六、解答题（每小题10分，共20分）

25. 如图，在 $△ A B C$ 中， $A B = A C = 2$ ， $∠ B = 40 °$ ，点D在线段BC上运动（点D不与点B ， C重合），连接AD ，作 $∠ A D E = 40 °$ ， DE交线段AC于点E ．

(1)、当 $∠ B D A = 115 °$ 时， $∠ E D C =$ °

(2)、线段DC的长度为何值时， $△ A B D ≌ △ D C E$ ，请说明理由；

(3)、在点D的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，求出 $∠ B D A$ 的度数；若不可以，请说明理由．

查看试题解析
26. 如图，在 $△ A B C$ 中， $∠ A C B = 60 °$ ，点D为 $△ A B C$ 边AC上一点， $B C = C D$ ，点M在BC的延长线上，CE平分 $∠ A C M$ ，且 $A C = C E$ ．连接BE交AC于F ， G为边CE上一点，满足 $C G = C F$ ，连接DG交BE于H ．

(1)、 $△ A B C ≌ △ E D C$ 吗？为什么？

(2)、求 $∠ D H F$ 的度数；

(3)、若EB平分 $∠ D E C$ ，则BE平分 $∠ A B C$ 吗？请说明理由．

查看试题解析