吉林省长春市德惠四中、五中、二十九中2023-2024学年八年级上学期数学期末考试模拟试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题（共6小题，满分12分，每小题2分）

1. 如所示四幅图案中，不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 计算3²⁰¹³•（ $\frac{1}{3}$ ）²⁰¹⁵的结果是（）

A、9 B、 $\frac{1}{3}$ C、2 D、 $\frac{1}{9}$

查看试题解析
3. 在平面直角坐标系中，点（﹣5，6）关于x轴对称的点在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内CD上方的一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β.下列各式：①α+β，②α﹣β，③β﹣α，④180°﹣α﹣β，⑤360°﹣α﹣β中，∠AEC的度数可能是（　　）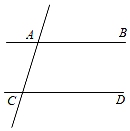

A、①②③ B、①②④⑤ C、①②③⑤ D、①②③④⑤

查看试题解析
5. 课本107页，画∠AOB的角平分线的方法步骤是：
①以O为圆心，适当长为半径作弧，交OA于M点，交OB于N点；
②分别以M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径作弧，两弧在∠AOB的内部相交于点C；
③过点C作射线OC．
射线OC就是∠AOB的角平分线．
请你说明这样作角平分线的根据是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
6. 在我市“绿水青山”行动中，某工程队承接了6万平方米的河滩绿化任务，为了应对雨季的到来，实际工作效率比原计划提高了20%，结果提前20天完成了这项任务．设实际每天的绿化面积为x万平方米，则下面所列方程中正确的是（　　）

A、 $\frac{6}{x} - \frac{6}{(1 + 20 %) x} = 20$ B、 $\frac{6}{(1 + 20 %) x} - \frac{6}{x} = 20$ C、 $\frac{6 (1 + 20 %)}{x} - \frac{6}{x} = 20$ D、 $\frac{6}{x} - \frac{6 (1 + 20 %)}{x} = 20$

查看试题解析

二、填空题（共8小题，满分24分，每小题3分）

7. 计算： $(\frac{1}{2})^{2020} \times (- 2)^{2020} =$ ．

查看试题解析
8. 式子① $\frac{2}{x}$ ， ② $\frac{x + y}{5}$ ， ③ $\frac{1}{2 - a}$ ， ④ $\frac{x}{π - 1}$ ， ⑤ $\frac{1}{m}$ （x+y）中，是分式的有．

查看试题解析
9. 如图，在Rt△ABC中，若∠C＝90°，D是BC边上的一点，且AD＝2CD ，则∠ADB的度数是．

查看试题解析
10. 在学习完“探索全等三角形全等的条件”一节后，一同学总结出很多全等三角形的模型，他设计了以下问题给同桌解决：如图，做一个“U”字形框架PABQ ，其中AB＝42cm ， AP ， BQ足够长，PA⊥AB于点A ，点M从B出发向A运动，同时点N从B出发向Q运动，点M ， N运动的速度之比为3：4，当两点运动到某一瞬间同时停止，此时在射线AP上取点C ，使△ACM与△BMN全等，则线段AC的长为 cm ．

查看试题解析
11. 已知当x＝﹣3时，ax³﹣bx+5＝9，则x＝3时，ax³﹣bx+9的值为．

查看试题解析
12. 如图，等腰△ABC中，AB＝AC，AC的垂直平分线分别交AB、AC于点D、E，BD的垂直平分线交AB于点F，并且恰好经过点C，则∠A＝°.

查看试题解析
13. 正八边形每个外角的度数为．

查看试题解析
14. 如图，一个边长为a、b（b＜a）的长方形被平行于边的两条直线所分割，其中长方形的左上角是一个边长为x的正方形，将图中阴影部分的面积S表示为S＝．

查看试题解析

三、解答题（共4小题，满分20分，每小题5分）

15. 计算：a（2﹣a）+（a+b）（a﹣b）．

查看试题解析
16. 阅读：分式 $\frac{3 x - 2}{x + 1}$ 可进行如下变形： $\frac{3 x - 2}{x + 1} = \frac{3 (x + 1) - 5}{x + 1} = 3 - \frac{5}{x + 1}$ ．

(1)、探索：如果 $\frac{5 x - 3}{x + 2} = 5 + \frac{m}{x + 2}$ ，则m＝；

(2)、总结：如果 $\frac{a x + b}{x + c} = a + \frac{m}{x + c}$ （其中a ， b ， c为常数），则m＝；

(3)、应用：利用上述结论解决：若代数式 $\frac{4 x - 3}{x - 1}$ 的值为整数，求满足条件的整数x的值．

查看试题解析
17. 下图是由5张全等的正方形组成的，请你补上一个正方形，使它变成轴对称图形．（用四种不同的方法）

查看试题解析
18. 一艘轮船沿江顺流航行100千米和逆流航行60千米所有的时间相同．已知水流的速度是5千米/时，求轮船在静水中的速度．

查看试题解析

四、解答题（共4小题，满分28分，每小题7分）

19. 如图，在四边形ABCD中，AB∥CD，∠1＝∠2，AD＝EC.

(1)、求证：△ABD≌△EDC；

(2)、若AB＝2，BE＝3，求CD的长.

查看试题解析
20. 先化简，再求值， $\frac{3 x + 3}{x - 1} \div (x + \frac{3 x + 1}{x - 1})$ ，其中x $= \sqrt{3} -$ 1．

查看试题解析
21. 如图，△ABC的三个顶点的坐标分别为A（1，2），B（3，1），C（2，4）．

(1)、在平面直角坐标系中作出△ABC关于y轴对称的△A^'B^'C^' ，并写出点A的对应点A^' ．

(2)、在（1）的条件下，求△CBB^'的面积．

查看试题解析
22. 如图所示，有块长为20米，宽为10米的长方形土地，现在将三面留出宽都是x米的小路，余下的长方形（阴影部分）做菜地．

(1)、用含x的式子表示：菜地的水平边长a＝米，菜地的周长C＝米；（结果化为最简形式）

(2)、现要沿菜地四周围上木栅栏，已知小路宽为1.5米，且木栅栏每米10元，求购买木栅栏需要多少钱？

查看试题解析

五、解答题（共2小题，满分16分，每小题8分）

23. 我们经常遇到需要分类的问题，画“树形图”可以帮我们不重复、不遗漏地分类．
【例题】在等腰三角形ABC中，若∠A＝80°，求∠B的度数．
分析：∠A、∠B都可能是顶角或底角，因此需要分成如图1所示的3类，这样的图就是树形图，据此可求出∠B＝50°、80°或20°．
【问题解决】已知等腰三角形ABC周长为19，AB＝7，仿照例题画出树形图，并直接写出BC的长度．

查看试题解析
24. 综合与探究
观察以下各式：
（x﹣y）（x+y）＝x²﹣y² ．
（x﹣y）（x²+xy+y²）＝x³﹣y³ ．
（x﹣y）（x³+x²y+xy²+y³）＝x⁴﹣y⁴ ．
（x﹣y）（x⁴+x³y+x²y²+xy³+y⁴）＝x⁵﹣y⁵ ．
请回答以下问题：

(1)、填空：（x﹣y）（x⁶+x⁵y+x⁴y²+x³y³+x²y⁴+xy⁵+y⁶）＝．

(2)、若n≥2，求证：6ⁿ﹣2ⁿ一定能被4整除．

(3)、求 $\frac{1 0^{20}}{9} -$ 10¹⁹﹣10¹⁸﹣10¹⁷﹣10¹⁶﹣…﹣10²﹣10﹣1的值．

查看试题解析

六、解答题（共2小题，满分20分，每小题10分）

25. 已知A ， B两地相距72千米，甲、乙两人骑自行车分别从A ， B两地相向而行，乙的速度是甲的速度的1.2倍，如果甲比乙先行 $\frac{2}{5}$ 小时，那么两人相遇时所行路程恰好相等．甲、乙两人骑自行车的速度各是多少？

查看试题解析
26. 如图，在平面直角坐标系中，A（12，0），B（0，9），动点M从点A出发沿AO以每秒2个单位长度的速度向原点O运动，同时动点N从点B出发沿折线BO﹣OA向终点A运动，点N在y轴上的速度是每秒3个单位长度，在x轴上的速度是每秒4个单位长度，过点M作x轴的垂线交AB于点C ，连接MN、CN ．点M和N都到达终点时，停止运动．设点M运动的时间为t（秒），△MCN面积为S（平方单位）．

(1)、当t为何值时，点M ， N相遇？

(2)、求△MCN的面积S（平方单位）与时间t（秒）的函数关系式；

(3)、直接写出当t为何值时，△MCN是等腰三角形．

查看试题解析