浙江省宁波市奉化区重点中学2023-2024学年八年级上学期期中数学试卷
试卷更新日期:2024-02-01 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 等腰三角形的两边长分别为3和6,则这个三角形的周长是( )A、15 B、12 C、12或15 D、93. 如图, , 要说明≌ , 添加的条件不能是( )
2. 等腰三角形的两边长分别为3和6,则这个三角形的周长是( )A、15 B、12 C、12或15 D、93. 如图, , 要说明≌ , 添加的条件不能是( )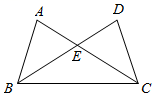 A、 B、 C、 D、4. 设 , 则下面不等式正确的是( )A、 B、 C、 D、5. 由下列条件不能判断△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:5 B、AB:BC:AC=3:4:5 C、∠A+∠B=∠C D、AB2=BC2+AC26. 尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP,由作法可得△OCP≌△ODP,判定这两个三角形全等的根据是( )
A、 B、 C、 D、4. 设 , 则下面不等式正确的是( )A、 B、 C、 D、5. 由下列条件不能判断△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:5 B、AB:BC:AC=3:4:5 C、∠A+∠B=∠C D、AB2=BC2+AC26. 尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP,由作法可得△OCP≌△ODP,判定这两个三角形全等的根据是( ) A、SAS B、ASA C、AAS D、SSS7. 在平面直角坐标系内,线段的两个端点坐标分别为、 , 平移线段得到线段 , 若点的对应点的坐标为 , 则的坐标为( )A、 B、 C、 D、8. 能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是( )A、 B、 C、 D、9. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC , AB边于E , F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A、SAS B、ASA C、AAS D、SSS7. 在平面直角坐标系内,线段的两个端点坐标分别为、 , 平移线段得到线段 , 若点的对应点的坐标为 , 则的坐标为( )A、 B、 C、 D、8. 能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是( )A、 B、 C、 D、9. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC , AB边于E , F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )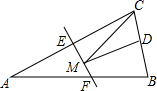 A、6 B、8 C、10 D、1210. 如图,分别以直角三角形的三边向外作等腰直角三角形,然后将较小的两个等腰直角和放在最大的等腰直角内如图 , 与交于点 , 连结 , 若要求的面积,只需要知道下列哪个三角形的面积即可( )
A、6 B、8 C、10 D、1210. 如图,分别以直角三角形的三边向外作等腰直角三角形,然后将较小的两个等腰直角和放在最大的等腰直角内如图 , 与交于点 , 连结 , 若要求的面积,只需要知道下列哪个三角形的面积即可( )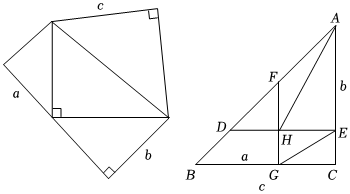 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题4分,共32分。
-
11. “x的2倍与3的差是非负数.”用不等式表示为: .12. 已知等腰三角形一个外角等于 , 则这个等腰三角形的顶角的度数是 .13. “对顶角相等”的逆命题是 . (用“如果…那么…”的形式写出)14. 在平面直角坐标系中,将点向右平移个单位长度得到点 , 则点关于轴的对称点的坐标是 .15. 如图,中,是的垂直平分线,交于 , 交于 , 已知 , 的周长为 , 则的周长是 .
 16. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=.
16. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=. 17. 若关于的不等式组的整数解共有个,则的取值范围是 .18. 如图,中, , , , 射线与边交于点 , 、分别为、中点,设点、到射线的距离分别为、 , 则线段的最小值为 ,的最大值为 .
17. 若关于的不等式组的整数解共有个,则的取值范围是 .18. 如图,中, , , , 射线与边交于点 , 、分别为、中点,设点、到射线的距离分别为、 , 则线段的最小值为 ,的最大值为 .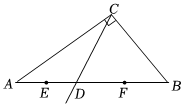
三、解答题:本题共6小题,共58分。解答应写出文字说明,证明过程或演算步骤。
-
19. 解不等式组 , 并把解集表示在数轴上.20. 如图,在平面直角坐标系中, , , .
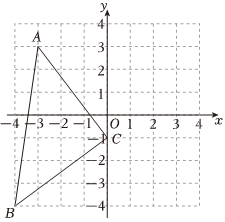 (1)、在图中作出关于轴对称的;(2)、在图中作出三角形中边上的中线;(3)、求的面积.21. 如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上.
(1)、在图中作出关于轴对称的;(2)、在图中作出三角形中边上的中线;(3)、求的面积.21. 如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上. (1)、求证:△DAB≌△ECB;(2)、若AD=3,AF=1,求BE的长.22. 如图,中, , , 是边上一点,且 , 若求的长.
(1)、求证:△DAB≌△ECB;(2)、若AD=3,AF=1,求BE的长.22. 如图,中, , , 是边上一点,且 , 若求的长. 23. 某校为提高学生的阅读品味,现决定购买获得第十届茅盾文学奖的北上徐则臣著和牵风记徐怀中著两种书共本已知购买本北上与购买本牵风记的价格相同;购买本北上和本牵风记需元.(1)、求这两种书的单价;(2)、若购买北上的数量不少于所购买牵风记数量的一半,且购买两种书的总价不超过元请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,如图 , 等腰与等腰中, , , , 我们把它们构成的这个图形叫做“手拉手模型”.
23. 某校为提高学生的阅读品味,现决定购买获得第十届茅盾文学奖的北上徐则臣著和牵风记徐怀中著两种书共本已知购买本北上与购买本牵风记的价格相同;购买本北上和本牵风记需元.(1)、求这两种书的单价;(2)、若购买北上的数量不少于所购买牵风记数量的一半,且购买两种书的总价不超过元请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,如图 , 等腰与等腰中, , , , 我们把它们构成的这个图形叫做“手拉手模型”.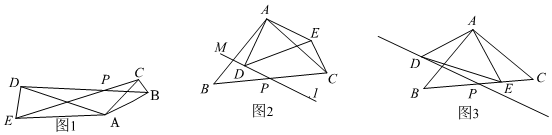 (1)、【模型探究】
(1)、【模型探究】如图 , 线段与线段存在怎样的数量关系?请证明你的结论.
(2)、【应用模型】如图 , 等腰直角三角形中, , , 点是边的中点,直线经过点 , 且 , 点是直线上的动点,将线段绕点顺时针旋转 , 得到线段 , 连结 .
如图 , 当点落在边上时,求 .
直接写出在点运动过程中,点和点之间的最短距离.