湖北省襄阳重点中学2023-2024学年七年级（上）数学期中试卷

试卷更新日期：2024-02-01 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. $- \frac{1}{2}$ 的绝对值是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $- 2$ D、 $2$

查看试题解析
2. 如图，数轴上有 $A$ 、 $B$ 、 $C$ 、 $D$ 四个点，其中表示互为相反数的点是（）

A、点 $A$ 与点 $D$ B、点 $A$ 与点 $C$ C、点 $B$ 与点 $C$ D、点 $B$ 与点 $D$

查看试题解析
3. 2022年2月13日，我国自营勘探开发的首个1500米超深水大气田“深海一号”在海南岛东南陵水海域正式投产，每年将向粤港琼等地稳定供气30亿立方米，可满足粤港澳大湾区四分之一的民生用气需求．将数据30亿用科学记数法表示应为3×10ⁿ ，则n的值为（）

A、7 B、8 C、9 D、10

查看试题解析
4. 下列说法中，错误的是（）

A、 $- 3$ 是负有理数 B、 $0$ 不是整数 C、 $\frac{1}{3}$ 是正有理数 D、 $- 0.15$ 是负分数

查看试题解析
5. 下列各组式子中是同类项的是（）

A、 $3 y$ 与 $3 x$ B、 $- x y^{2}$ 与 $\frac{1}{4} y x^{2}$ C、 $a^{3}$ 与 $2^{3}$ D、 $6$ 与 $- \frac{1}{6}$

查看试题解析
6. 我国是最早认识负数，并进行相关运算的国家．在古代数学名著《九章算术》里，就记载了利用算筹实施“正负术”的方法，图1表示的是计算3+（-4）的过程．按照这种方法，图2表示的过程应是在计算（）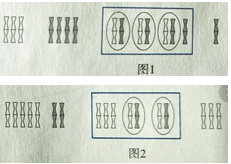

A、（-5）+（-2） B、（-5）+2 C、5+（-2） D、5+2

查看试题解析
7. 近似数7.55万精确到（）

A、百分位 B、个位 C、百位 D、万位

查看试题解析
8. 下列说法中正确的是（）

A、单项式 $\frac{- 3 x^{2} y}{2}$ 的系数是 $- 3$ B、 $- x y z^{2}$ 的次数是 $2$ C、 $2 x^{3} - 8 x^{2} + x$ 是二次三项式 D、单项式 $- 2 x n^{3}$ 的系数是 $- 2$ ，次数是 $4$

查看试题解析
9. 有理数 $a$ ， $b$ 在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $a + b > 0$ B、 $a b > 0$ C、 $b - a < 0$ D、 $| a | > | b |$

查看试题解析
10. 用木棒按如图所示的规律摆放图形，第100个图形需要木棒根数是（）

A、501 B、502 C、503 D、504

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 已知一只蚂蚁的左边5米有一块食物，记该食物的位置为+5米，那么食物在蚂蚁右边3米处，应为米．

查看试题解析
12. 比较大小 $($ 用“ $<$ ”“ $=$ ”或“ $>$ ”填空 $)$ ： $- \frac{5}{9}$ $- \frac{3}{5}$ ．

查看试题解析
13. 若 $a$ ， $b$ 互为倒数， $c$ ， $d$ 互为相反数，则 $c + d - 2 (a b)^{2023} =$ ．

查看试题解析
14. 某种商品的原价每件a元，第一次降价打“八折”，第二次降价又减10元，则两次降价后的售价为．

查看试题解析
15. 定义：若 $a - b = 0$ ，则称 $a$ 与 $b$ 互为平衡数，若 $2 x^{2} - 2$ 与 $x + 4$ 互为平衡数，则代数式 $4 x^{2} - 2 x - 11 =$ ．

查看试题解析
16. 若 $| x | = 7$ ， $| y | = 3$ ，且 $x > y$ ，则 $y - x$ 等于．

查看试题解析

三、计算题：本大题共1小题，共12分。

17. 计算：

(1)、 $12 - (- 18) + (- 7) - 15$ ；

(2)、 $(- 81) \div \frac{9}{4} \times \frac{4}{9} \div (- 16)$ ；

(3)、 $(1 \frac{3}{4} - \frac{7}{8} + \frac{7}{12}) \div (- \frac{1}{24})$ ；

(4)、 $- 1^{4} + [\frac{2}{3} \times (- 6) - (- 3)^{2}] \div 2$ ．

查看试题解析

四、解答题：本题共7小题，共40分。解答应写出文字说明，证明过程或演算步骤。

18. 化简：

(1)、 $- 3 x y - 2 y^{2} + 5 x y - 4 y^{2}$ ；

(2)、 $- 5 + (x^{2} + 3 x) - (- 9 + 6 x^{2}) .$

查看试题解析
19. 在给定的数轴上表示下列各数，并用“ $<$ ”符号将它们连接起来：
$- 4$ ， $| - 2.5 |$ ， $- | + 3 |$ ， $- 1 \frac{1}{2}$ ， $- (- 1)$ ．

查看试题解析
20. 先化简，再求值： $\frac{1}{2} a - 2 (a - \frac{1}{3} b^{2}) + (- \frac{3}{2} a + \frac{1}{3} b^{2})$ ，其中 $(a + 3)^{2} + | b + \frac{1}{2} | = 0$ ．

查看试题解析
21. 已知代数式 $A = 3 x^{2} - 4 x + 2$ ．

(1)、若 $B = x^{2} - 2 x - 1$ ，求 $A - 2 B$ ；

(2)、若 $B = a x^{2} - x - 1 (a$ 为常数 $)$ ，且 $A$ 与 $B$ 的和不含 $x^{2}$ 页，求整式 $4 a^{2} + 5 a - 2$ 的值．

查看试题解析
22. $2022$ 年卡塔尔世界杯期间，某电商平台直播间从开幕式第一天起开启了为期一周的直播公益活动，活动如下：每销售一只世界杯吉祥物“拉伊卜”，就从销售额里拿出一部分作为慈善基金捐赠给某希望中学用于购买学生体育用品 $.$ 规定当天吉祥物销售量超过 $300$ 只的部分记为“ $+$ ”，低于 $300$ 只的部分记为“ $-$ ”，下表是公益活动一周的销售量：
时间
$11.21$
$11.22$
$11.23$
$11.24$
$11.25$
$11.26$
$11.27$
销售量超过部分
$($ 单位：只 $)$
$200$
$180$
$220$
$- 50$
$- 100$
$160$
$90$

(1)、求这一周公益活动期间的“拉伊卜”总销售量？

(2)、吉祥物“拉伊卜”的销售单价是 $120$ 元，捐赠方案如下：每天销售量中不超过 $300$ 只的部分，按每只销售价的 $1 %$ 捐赠；每天销售量中超过 $300$ 只的部分，按每只销售价的 $2 %$ 捐赠 $.$ 求直播公益活动期间一共捐赠了多少钱？

查看试题解析
23. 如图是某小区的一块长为 $a$ 米、宽为 $2 b$ 米的长方形空地，为美化环境，准备在这个长方形空地的四个顶点处分别修建一个半径为 $b$ 米的扇形花台 $(\frac{1}{4}$ 圆 $)$ ，然后在花台内种花，其余种草 $.$ 如果建造花台及种花的费用为每平米 $100$ 元，种草的费用为每平米 $50$ 元．

(1)、直接写出草坪 $($ 阴影部分 $)$ 的面积平方米 $($ 用含 $a$ ， $b$ 和的式子表示 $)$ ；

(2)、求美化这块空地共需多少元？ $($ 用含 $a$ ， $b$ 和 $π$ 的式子表示 $)$

(3)、 $a = 6$ ， $b = 2$ ，美化这块空地共需多少元？ $(π$ 取 $3.14)$

查看试题解析

24. 甲、乙两人借助“数轴”和“剪刀、石头、布”设计了一款“移动游戏”

.

两人分别在数轴上随机挑选一个点作为游戏的起点：甲选择的游戏起点记为

A

，乙选择的游戏起点记为

B

；然后两人进行“剪刀、石头、布”，每次“剪刀、石头、布”的结果共有三种可能：平局、甲胜、乙胜；再根据每次“剪刀、石头、布”的结果，

A

、

B

两点沿数轴同时移动，移动规则如下：

“剪刀、石头、布”的结果	A、 $B$ 两点移动方式
平局	点 $A$ 向右移动 $0.5$ 个单位，点 $B$ 向左移动 $0.5$ 个单位
甲胜	点 $A$ 向右移动 $2$ 个单位，点 $B$ 向右移动 $1$ 个单位
乙胜	点 $A$ 向左移动 $1$ 个单位，点 $B$ 向左移动 $2$ 个单位

设甲、乙两人共进行了 $k$ 次“剪刀、石头、布” $(k$ 为正整数 $)$ ．

(1)、如图，起点

A

表示的数是

- 5

，起点

B

表示的数是

3

．

$①$ 当 $k = 3$ 时，其中平局一次，甲胜一次，点 $A$ 最终位置表示的数为，点 $B$ 最终位置表示的数为，此时 $A$ 、 $B$ 两点间的距离为．

$②$ 当 $k = 10$ 时，其中平局 $x$ 次，甲胜 $y$ 次，求 $A$ 、 $B$ 两点最终位置表示的数 $. ($ 用含 $x$ 、 $y$ 的代数式表示 $)$

(2)、若起点

A

表示的数是

a

，起点

B

表示的数是

b (a

、

b

均为整数，且

a < b)

，当

A

、

B

两点最终位置相距

3

个单位时，探究

k

的值，直接写出结论

. (

用含

a

、

b

的代数式表示

)

查看试题解析