浙江省金华市东阳市横店八校联考2023-2024学年八年级上册12月月考数学试题

试卷更新日期：2024-02-01 类型：月考试卷

进入出卷网下载

一、选择题（本题共30分，每小题3分）

1. 下列四个数学符号中，是轴对称图形的是（）

A、 $≌$ B、 $\neq$ C、∴ D、 $\geq$

查看试题解析
2. 点 $(2023 ， - 2024)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 若长度分别为a ， 4，8的三条线段能组成一个三角形，则a的值可以是（）

A、4 B、8 C、12 D、16

查看试题解析
4. 下列函数中，属于正比例函数的是（）．

A、 $y = 2 x$ B、 $y = 2 x - 1$ C、 $y = \frac{2}{x}$ D、 $y = 2 x^{2}$

查看试题解析
5. 已知 $a + 3 > 0$ ，则下列四个不等式中一定成立的是（）

A、 $a + 1 < 0$ B、 $a - 1 < 0$ C、 $3 a > - 1$ D、 $\frac{a}{3} > - 1$

查看试题解析
6. 一副三角板，按如图所示叠放在一起，则图中 $∠ α$ 的度数是（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $75 °$

查看试题解析
7. 如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE．若AC=5，BC=3，则BD的长为（）

A、2.5 B、1.5 C、2 D、1

查看试题解析
8. 某业主贷款2.2万元购进一台机器，生产某种产品．已知产品的成本是每个5元，售价是每个8元，应付的税款和其他费用是售价的10%，若每个月能生产、销售2000个产品，问至少几个月后能赚回这台机器的贷款？（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图，已知 $∠ A O B = 30 °$ ，点P在边OA上，OP＝4，点M ， N在边OB上，PM＝PN ，且 $∠ M P N = 90 °$ ，则 $O N =$ （）

A、8 B、6 C、 $\sqrt{12} + 2$ D、 $\sqrt{12} + 4$

查看试题解析
10. 如图，把直线y=－2x向上平移后得到直线AB，直线AB经过点(m，n)，且2m＋n=6，则直线AB的解析式是（）

A、y=－2x－3 B、y=－2x－6 C、y=－2x＋3 D、y=－2x＋6

查看试题解析

二、填空题（本题共24分，每小题4分）

11. 命题“直角三角形两锐角互余”的逆命题是：．

查看试题解析
12. 已知点 $P_{1} (a + 1 ， 3)$ 和点 $P_{2} (2 ， b)$ 关于y轴对称，则 $a + b$ 的值为．

查看试题解析
13. 已知直角三角形的两条边长为4和5，则此直角三角形斜边上的中线长为．

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $C D ⊥ A B$ ， E为 $A B$ 中点．若 $B D = 2$ ，则 $A B =$ ．

查看试题解析
15. 如图，有一张长方形片ABCD， $A B = 8 cm$ ， $B C = 10 cm$ ．点E为CD上一点，将纸片沿AE折叠，BC的对应边 $B^{'} C^{'}$ 恰好经过点D，则线段DE的长为cm．

查看试题解析
16. 如图，在长方形 $A B C D$ 中， $A B = 4 c m$ ， $A D = 6 c m$ ， E为 $A B$ 的中点．点P从点D出发，以2cm/s的速度沿 $D \to C \to B \to A$ 路线运动，运动至点A停止，运动时间为t（s），若 $△ D E P$ 为等腰三角形，则t的值为．

查看试题解析

三、解答题（本题共66分）

17. 解不等式组： ${\begin{array}{l} x + 1 < 4 \\ 3 x - 12 \leq 5 x \end{array}$ ，并把解集表示在数轴上．

查看试题解析
18. 如图，在平面直角坐标系中， $△ O A B$ 三个顶点的坐标分别是 $O (0 ， 0)$ ， $A (2 ， 1)$ ）， $B (1 ， 3)$ ．

(1)、在图1中，以x轴为对称轴，作出 $△ O A B$ 的轴对称图形；

(2)、在图2中，把 $△ O A B$ 先向左平移4个单位，再向下平移2个单位得 $△ O^{'} A^{'} B^{'}$ ，请在图2中画出 $△ O^{'} A^{'} B^{'}$ ．

查看试题解析
19. 已知一次函数 $y = k x - 4$ ，当 $x = 2$ 时， $y = - 3$ ．

(1)、求一次函数的解析式；

(2)、求该一次函数与坐标轴围成的三角形的面积．

查看试题解析
20. 如图， $△ A B C$ 中， $A B = B C$ ， $∠ A B C = 90 °$ ， F为 $A B$ 延长线上一点，点E在 $B C$ 上，且 $A E = C F$ ．

(1)、求证： $△ A B E ≌ △ C B F$ ；

(2)、若 $∠ A C F = 65 °$ ，求 $∠ C A E$ 的度数．

查看试题解析
21. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．

(1)、问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；

(2)、求原来的路线AC的长．

查看试题解析
22. 为落实“垃圾分类”的环保理念，某学校同时购进绿色和灰色两种颜色的垃圾桶，若购进2个绿色垃圾桶和1个灰色垃圾桶共需280元；若购进3个绿色垃圾桶和2个灰色垃圾桶共需460元．

(1)、求绿色垃圾桶和灰色垃圾桶每个进价分别为多少元？

(2)、为创建垃圾分类示范学校，学校预计用不超过9000元的资金购入两种垃圾桶共计100个，且绿色垃圾桶数量不少于灰色垃圾桶数量的 $80 %$ ，请求出共有几种购买方案？

(3)、每购买一个绿色垃圾桶和灰色垃圾桶，政府分别补贴m元和n元，如果（2）中的所有购买方案费用相同，求m与n之间的数量关系．

查看试题解析
23. 概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.

从三角形 $($ 不是等腰三角形 $)$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.

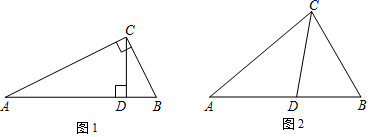(1)、理解概念
如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，请写出图中两对“等角三角形”

(2)、概念应用
如图2，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 °$ .
求证： $C D$ 为 $△ A B C$ 的等角分割线.

(3)、在 $△ A B C$ 中， $∠ A = 42 °$ ， $C D$ 是 $△ A B C$ 的等角分割线，直接写出 $∠ A C B$ 的度数.

查看试题解析
24. 如图1，直线l： $y = - \frac{3}{4} x + 6$ 分别与x ， y轴交于A ， B两点，作 $∠ A B O$ 的角平分线交x轴于点P ．

(1)、写出A ， B的坐标．

(2)、求 $O P$ 的长．

(3)、如图2，点C为线段BP上一点，过点C作 $C D ∥ A B$ 交x轴于点D ，且 $C D = O B$ ．求证：P为 $O D$ 中点．

查看试题解析