吉林省长春市绿园区2023-2024学年九年级上学期期末考试数学试题
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 二次根式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 二次函数的顶点坐标是( )A、 B、 C、 D、3. 下列二次根式中,能与合并的是( )A、 B、 C、 D、4. 如图,在 中, , , , ,则 的长为( )
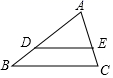 A、 B、 C、 D、5. 如图,在平面直角坐标系中,将点绕原点逆时针旋转得到点 , 则点的坐标为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,将点绕原点逆时针旋转得到点 , 则点的坐标为( ) A、 B、 C、 D、6. 如图, 与 位似,其位似中心为点 ,且 为 的中点,则 与 的面积比是( )
A、 B、 C、 D、6. 如图, 与 位似,其位似中心为点 ,且 为 的中点,则 与 的面积比是( )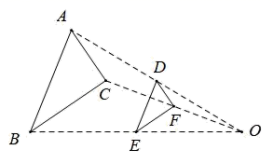 A、 B、 C、 D、7. 如图,电线杆直立在水平的地面上,是电线杆的一根拉线,测得 , , 则拉线的长为( )
A、 B、 C、 D、7. 如图,电线杆直立在水平的地面上,是电线杆的一根拉线,测得 , , 则拉线的长为( ) A、 B、 C、 D、8. 若抛物线的对称轴为轴,且点在该抛物线上,则的值为( )A、 B、0 C、2 D、4
A、 B、 C、 D、8. 若抛物线的对称轴为轴,且点在该抛物线上,则的值为( )A、 B、0 C、2 D、4二、填空题(本大题共6小题,每小题3分,共18分)
-
9. .10. 计算: .11. 已知关于的一元二次方程有一个根为 , 则的值为 .12. 若关于的方程有实数根,则的取值范围为 .13. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上,如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是 .
 14. 如图,一抛物线型拱桥的拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1.5米后,水面的宽度为米.
14. 如图,一抛物线型拱桥的拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1.5米后,水面的宽度为米.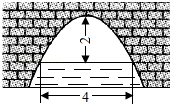
三、解答题(本大题共10小题,共78分)
-
15. 计算: .16. 解方程: .17. 某厂一月份产值为64万元,计划三月份产值要达100万元.若每个月的平均增长率相同,求平均增长率是多少.18. 在一个不透明的盒子中放有三张卡片,分别标记为、、 , 每张卡片除了标记不同外,其余均相同.某同学第一次从盒子中随机抽取一张卡片,卡片放回,第二次又随机抽取一张卡片,请用画树状图(或列表)的方法,求两次抽取的卡片完全相同的概率.19. 图①、图②均为的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的三个顶点均在格点上.只用无刻度的直尺,在图①、图②中各画一个与相似(相似比不为1),且不全等的三角形(要求三角形的顶点都在格点上)
 20. 如图, , , 点是线段上的一点,且 . 已知 , , .
20. 如图, , , 点是线段上的一点,且 . 已知 , , . (1)、求证: .(2)、求线段的长.21. 如图,抛物线与轴交于 , 两点,与轴交于点 , 抛物线的顶点为 .
(1)、求证: .(2)、求线段的长.21. 如图,抛物线与轴交于 , 两点,与轴交于点 , 抛物线的顶点为 . (1)、直接写出 , , , 四个点的坐标;(2)、求四边形的面积.22. 角平分线性质定理描述了角平分线上的点到角的两边距离的关系,小明发现将角平分线放在三角形中,还可以得出一些线段比例的关系.
(1)、直接写出 , , , 四个点的坐标;(2)、求四边形的面积.22. 角平分线性质定理描述了角平分线上的点到角的两边距离的关系,小明发现将角平分线放在三角形中,还可以得出一些线段比例的关系.
请完成下列探索过程:
(1)、【初步思考】如图1,在中,的角平分线交于点 . 若 , , 则;
(2)、【深入探究】如图1,在中,的角平分线交于点 . 求证:=;
(3)、【应用迁移】如图2,和都是等边三角形,的顶点在的边上,交于点 , 若 , , 直接写出的面积.
23. 如图,在中, , , , 动点从点出发,沿方向以每秒2个单位长度的速度向终点运动,点为线段的中点,过点向上作 , 且 , 以、为边作矩形 . 设点的运动时间为(t>0)秒. (1)、线段的长为(用含的代数式表示).(2)、当点N恰好落在边上时,求的值.(3)、当点在内部时,设矩形与重叠部分图形的面积为 , 求与之间的函数关系式.(4)、当点恰好落在的角平分线上时,直接写出的值.24. 在平面直角坐标系中,抛物线、是常数)经过点 , . 点在抛物线上,且点的横坐标为 .(1)、求该抛物线对应的函数表达式.(2)、求点关于抛物线、是常数)的对称轴对称的点的坐标(用含的代数式表示).(3)、当点在轴上方时,直接写出的取值范围.(4)、若此抛物线在点及点左侧部分的最低点的纵坐标为 , 求的值.
(1)、线段的长为(用含的代数式表示).(2)、当点N恰好落在边上时,求的值.(3)、当点在内部时,设矩形与重叠部分图形的面积为 , 求与之间的函数关系式.(4)、当点恰好落在的角平分线上时,直接写出的值.24. 在平面直角坐标系中,抛物线、是常数)经过点 , . 点在抛物线上,且点的横坐标为 .(1)、求该抛物线对应的函数表达式.(2)、求点关于抛物线、是常数)的对称轴对称的点的坐标(用含的代数式表示).(3)、当点在轴上方时,直接写出的取值范围.(4)、若此抛物线在点及点左侧部分的最低点的纵坐标为 , 求的值.