吉林省松原市前郭县2023-2024学年八年级上学期期末考试数学试题

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 第 $19$ 届亚运会于 $2023$ 年9月 $23$ 日- $2023$ 年 $10$ 月8日在中国杭州举行．下列四个图案是历届会徽图案，其中可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若一个三角形三个内角度数的比为 $2 ： 3 ： 5$ ，那么这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(a^{3})}^{2} = a^{6}$ D、 ${(- 2 a^{2})}^{3} = - 6 a^{6}$

查看试题解析
4. 下列分式中，最简分式是（）

A、 $\frac{4}{2 x}$ B、 $\frac{2 x}{x^{2} + 1}$ C、 $\frac{x - 1}{x^{2} - 1}$ D、 $\frac{x - 1}{1 - x}$

查看试题解析
5. 下列多项式相乘，能用平方差公式计算的是（）

A、 $(x + 2) (x + 2)$ B、 $(- x + y) (x - y)$ C、 $(2 x - y) (2 x + y)$ D、 $(- x - y) (x + y)$

查看试题解析
6. 小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线 $O B$ ，另一把直尺压住射线 $O A$ 并且与第一把直尺交于点 $P$ ，小明说：“射线 $O P$ 就是 $∠ B O A$ 的角平分线．”他这样做的依据是（）

A、在角的内部，到角的两边距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形的三条高交于一点 D、三角形三边的垂直平分线交于一点

查看试题解析

二、填空题（每小题3分，共24分）

7. 人体中枢神经系统中约含有1千亿个神经元，某种神经元的直径约为 $0.000052 m$ .将0.000052用科学记数法表示为.

查看试题解析
8. 当x时，分式 $\frac{x + 2}{x - 1}$ 有意义.

查看试题解析
9. 一个多边形的内角和与它的外角和之比为 $3 ： 1$ ，则这个多边形的边数是．

查看试题解析
10. 如图所示的是一款手机支架，能非常方便地支起手机，由图分析这款手机支架的设计原理是三角形的．

查看试题解析
11. 如图， $△ A B C ≌ △ D E C$ ，点B、C、D在同一直线上，且 $B D = 12$ ， $A C = 7$ ，则 $C E$ 长为．

查看试题解析
12. 一个长、宽分别为m、n的长方形的周长为16，面积为6，则 $m^{2} n + m n^{2}$ 的值为.

查看试题解析
13. 如图，将矩形纸片 $A B C D$ 沿 $E F$ 折叠，点C落在边 $A B$ 上的点H处，点D落在点G处，若 $∠ G E F = 111 °$ ，则 $∠ A H G$ 的度数为．

查看试题解析
14. 《九章算术》中有一道关于古代驿站送信的题目，其白话译文为：一份文件，若用慢马送到 $900$ 里远的城市，所需时间比规定时间多1天；若改为快马派送，则所需时间比规定时间少3天，已知快马的速度是慢马的2倍，求规定时间，设规定时间为x天，则可列出正确的方程为．

查看试题解析

三、解答题（每题5分，共20分）

15. 计算： $a^{9} \div a^{2} \cdot a + {(a^{2})}^{4} - {(- 2 a^{4})}^{2}$ ．

查看试题解析
16. 先化简分式 $(1 - \frac{1}{x - 2}) \div \frac{x^{2} - 6 x + 9}{2 x - 4}$ ，再从2≤x≤4中选一个合适的整数代入求值．

查看试题解析
17. 解方程 $\frac{1}{x + 3} - \frac{2}{3 - x} = \frac{12}{x^{2} - 9}$

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ B = 62 °$ ， $∠ A = 28 °$ ， $C E$ 平分 $∠ A C B$ ， $C D$ 是 $A B$ 上的高．求 $∠ D C E$ 的度数．

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，在长度为1个单位长度的小正方形组成的正方形网格纸中，点 $A 、 B 、 C$ 在小正方形的顶点上．

(1)、在图中画出与 $△ A B C$ 关于直线 $l$ 成轴对称的 $△ A^{'} B^{'} C^{'}$ ；

(2)、在 $l$ 上找一点 $P$ ，使得 $P A = P B$ ；

(3)、在 $l$ 上找一点 $Q$ ，使得 $Q B + Q C$ 最小．

查看试题解析
20. 观察以下等式：
第1个等式： $\frac{2}{3^{2} - 4} \times (2 - \frac{1 - 4}{1}) = \frac{2}{1}$ ；
第2个等式： $\frac{4}{4^{2} - 4} \times (2 - \frac{2 - 4}{2}) = \frac{2}{2}$ ；
第3个等式： $\frac{6}{5^{2} - 4} \times (2 - \frac{3 - 4}{3}) = \frac{2}{3}$ ；
第4个等式： $\frac{8}{6^{2} - 4} \times (2 - \frac{4 - 4}{4}) = \frac{2}{4}$ ；
第5个等式： $\frac{10}{7^{2} - 4} \times (2 - \frac{5 - 4}{5}) = \frac{2}{5}$ ；……
按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第 $n$ 个等式： ▲ （用含 $n$ 的等式表示），并证明．

查看试题解析
21. 某建筑测量队为了测量一栋居民楼ED的高度，在大树AB与居民楼ED之间的地面上选了一点C，使B，C，D在一直线上，测得大树顶端A的视线AC与居民楼顶端E的视线EC的夹角为90°，若AB=CD=12米，BD=64米，请计算出该居民楼ED的高度.

查看试题解析
22. 在理解例题的基础上，完成下列两个问题：
例题：若 $m^{2} + 2 m n + 2 n^{2} - 4 n + 4 = 0$ ，求m和n的值；
解：由题意得： $(m^{2} + 2 m n + n^{2}) + (n^{2} - 4 n + 4) = 0$ ，
∴ ${(m + n)}^{2} + {(n - 2)}^{2} = 0$ ∴ ${\begin{array}{l} m + n = 0 \\ n - 2 = 0 \end{array}$ ，解得 ${\begin{array}{l} m = - 2 \\ n = 2 \end{array}$ ．
请解决以下问题：

(1)、若 $x^{2} + 4 x y + 5 y^{2} - 4 y + 4 = 0$ ，求 $y^{x}$ 的值；

(2)、若a，b，c是 $△ A B C$ 的边长，满足 $a^{2} + b^{2} = 12 a + 8 b - 52$ ， c是 $△ A B C$ 的最长边，且c为奇数，则c可能取何值？

查看试题解析

五、解答题（每小题8分，共16分）

23. 数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：

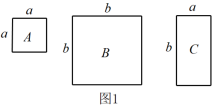
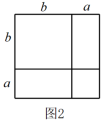
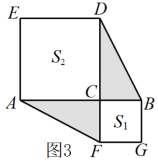(1)、由图1和图2可以得到的等式为（用含a，b的等式表示）；

(2)、莉莉想用这三种纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 的大长方形，求需A，B，C三种纸片各多少张；

(3)、如图3，S₁ ， S₂分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上， $S_{1} + S_{2} = 20$ ， $p + q = 6$ ．求图中阴影部分的面积．

查看试题解析
24. 如图

(1)、【探究与发现】如图1， $A D$ 是 $△ A B C$ 的中线，延长 $A D$ 至点E，使 $E D = A D$ ，连接 $B E$ ，写出图中全等的两个三角形．

(2)、【理解与应用】填空：如图2， $E P$ 是 $△ D E F$ 的中线，若 $E F = 5$ ， $D E = 3$ ，设 $E P = x$ ，则x的取值范围是．

(3)、已知：如图3， $A D$ 是 $△ A B C$ 的中线， $∠ B A C = ∠ A C B$ ，点Q在 $B C$ 的延长线上， $Q C = B C$ ，求证： $A Q = 2 A D$ ．

查看试题解析

六、解答题（每小题10分，共20分）

25. 为提升青少年的身体素质，郑州市在全市中小学推行“阳光体育”活动，河南省实验中学为满足学生的需求，准备再购买一些篮球和足球．如果分别用800元购买篮球和足球，购买篮球的个数比足球的个数少2个，足球的单价为篮球单价的 $\frac{4}{5}$ ．

(1)、求篮球、足球的单价分别为多少元？

(2)、学校计划用不多于5200元购买篮球、足球共60个，那么至少购买多少个足球？

(3)、在（2）的条件下，若篮球数量不能低过15个，那么有多少种购买方案？哪种方案费用最少？最少费用是多少？

查看试题解析
26. 在等边 $△ A B C$ 中， $A C = 8$ ，动点P以每秒3个单位长度的速度从点A出发在射线 $A C$ 上运动，设点P的运动时间为t秒．

(1)、用含t的代数式表示线段 $C P$ 的长；

(2)、连结 $P B$ ，当 $∠ P B C = 30 °$ 时，求t的值；

(3)、若在线段 $B C$ 上存在一点D，且 $C D = 6$ ．在点P运动的同时有一动点Q以每秒2个单位长度的速度从点C出发在线段 $C D$ 上运动，当点Q运动到点D时，立即以原速度返回至终点C，当 $△ C P Q$ 为等腰三角形时，直接写出t的值．

查看试题解析