吉林省长春市榆树市2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-01 类型:期末考试
一、选择题:(每小题3分,共24分)
-
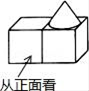
1. ﹣5的绝对值是( )A、5 B、﹣5 C、 D、2. 据统计,国家“一带一路”倡议将产生 美元的经济效益,数据 用科学记数法可表示为( )A、 B、 C、 D、3. 如图是一个由两个小正方体和一个圆锥组成的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、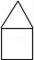 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 不改变多项式2b3﹣5ab2+4a2b﹣1的值,把后三项放在前面是“﹣”号的括号中,正确的是( )A、2b3﹣(5ab2﹣4a2b+1) B、2b3﹣(5ab2+4a2b+1) C、2b3﹣(﹣5ab2+4a2b﹣1) D、2b3﹣(5ab2+4a2b﹣1)6. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 不改变多项式2b3﹣5ab2+4a2b﹣1的值,把后三项放在前面是“﹣”号的括号中,正确的是( )A、2b3﹣(5ab2﹣4a2b+1) B、2b3﹣(5ab2+4a2b+1) C、2b3﹣(﹣5ab2+4a2b﹣1) D、2b3﹣(5ab2+4a2b﹣1)6. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )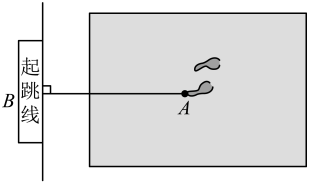 A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直7. 下列各图中,过直线l外一点P画它的垂线CD , 三角板操作正确的是( )A、
A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直7. 下列各图中,过直线l外一点P画它的垂线CD , 三角板操作正确的是( )A、 B、
B、 C、
C、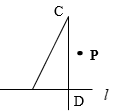 D、
D、 8. 如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东 , 甲、乙两地同时开工,要使若干天后公路准确接通,乙地所修的公路走向是( )
8. 如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东 , 甲、乙两地同时开工,要使若干天后公路准确接通,乙地所修的公路走向是( )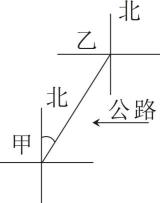 A、北偏东 B、南偏西 C、北偏东 D、南偏西
A、北偏东 B、南偏西 C、北偏东 D、南偏西二、填空题:(每小题3分,共18分)
-
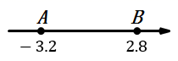
9. 若m与-2互为相反数,则m的值为。10. 多项式ab3-3a2b-a3b-3按字母a降幂排列是 .11. 计算: 度.12. 如图,在数轴上,点A与点B之间表示整数的点有个.
 13. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)
13. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)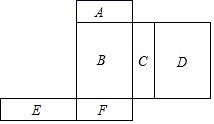 14. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第1个图形一共有5个实心圆点,第2个图形一共有8个实心圆点,第3个图形一共有11个实心圆点,….按此规律排列下去,第n个图形中实心圆点的个数为 (用含n的代数式表示).
14. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第1个图形一共有5个实心圆点,第2个图形一共有8个实心圆点,第3个图形一共有11个实心圆点,….按此规律排列下去,第n个图形中实心圆点的个数为 (用含n的代数式表示).
三、解答题:(本大题共10小题,共78分)
-
15. 计算:(1)、(2)、 .16. 计算:(1)、(2)、17. 先化简,再求值: , 其中x=1,y=−1.18. 如图,在的正方形网格中,每个小正方形的边长均为1,其顶点称为格点,点A、B、C、D均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
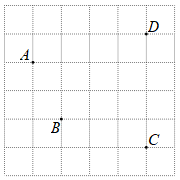 (1)、画直线 .(2)、画射线 .(3)、画线段 .(4)、在线段上确定一点E,使 .19. 已知多项式A=2m2﹣4mn+2n2 , B=m2+mn﹣3n2 , 求:(1)、3A+B;(2)、A﹣3B.20. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
(1)、画直线 .(2)、画射线 .(3)、画线段 .(4)、在线段上确定一点E,使 .19. 已知多项式A=2m2﹣4mn+2n2 , B=m2+mn﹣3n2 , 求:(1)、3A+B;(2)、A﹣3B.20. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.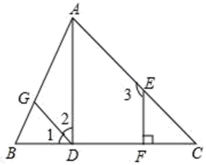
解:∵∠1=∠C,(已知)
∴GD∥ ▲ . ( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC=∠ ▲ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
21. 如图,直线AB,CD相交于点O,过点O作OE⊥AB,OF平分∠BOD。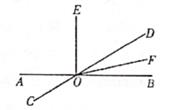 (1)、直接写出∠AOC的补角;(2)、若∠AOC=40°,求∠EOF的度数。22. 如图所示,两种长方形断桥铝窗框,已知窗框的长都是 米,宽都是 米,已知一用户需A型的窗框4个,B型的窗框3个.
(1)、直接写出∠AOC的补角;(2)、若∠AOC=40°,求∠EOF的度数。22. 如图所示,两种长方形断桥铝窗框,已知窗框的长都是 米,宽都是 米,已知一用户需A型的窗框4个,B型的窗框3个.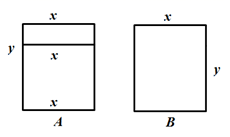 (1)、用含 、 的式子表示共需断桥铝的长度(窗框本身宽度忽略不计)(2)、若1米断桥铝的平均费用为200元,求当 , 时,(1)中断桥铝的总费用为多少元?23. 【教材呈现】下面是华题版七年级上册数学教材第页部分内容.C组17.代数式的值为7,则代数式的值为 ▲ .
(1)、用含 、 的式子表示共需断桥铝的长度(窗框本身宽度忽略不计)(2)、若1米断桥铝的平均费用为200元,求当 , 时,(1)中断桥铝的总费用为多少元?23. 【教材呈现】下面是华题版七年级上册数学教材第页部分内容.C组17.代数式的值为7,则代数式的值为 ▲ .【阅读理解】小明在做作业时采用的方法如下:
由题意,得 , 则有 ,
所以代数式的值为5.
(1)、【方法运用】若代数式的值为 , 求代数式的值.(2)、当时,的值为9,当时,求的值.(3)、【拓展应用】若 , , 则代数式的值为 .24. 如图
 (1)、【问题】如图①,线段 , 点是线段上一点,点、分别是线段、的中点,求线段的长(请写出说理步骤).(2)、【拓展】如图①,线段 , 点是线段上一点,点、分别是线段、的中点,则线段的长为cm.用含字母的代数式表示)(3)、【应用】如图②, , 射线是内部任一射线,射线、分别平分、 , 则的大小为 . 用含字母的代数式表示(4)、如图③, , , 点是线段上一点与点、不重合 , 、分别平分、 , 分别交射线于点 , . 求与的差.
(1)、【问题】如图①,线段 , 点是线段上一点,点、分别是线段、的中点,求线段的长(请写出说理步骤).(2)、【拓展】如图①,线段 , 点是线段上一点,点、分别是线段、的中点,则线段的长为cm.用含字母的代数式表示)(3)、【应用】如图②, , 射线是内部任一射线,射线、分别平分、 , 则的大小为 . 用含字母的代数式表示(4)、如图③, , , 点是线段上一点与点、不重合 , 、分别平分、 , 分别交射线于点 , . 求与的差.