吉林省长春市绿园区2023-2024学年七年级上学期期末考试数学试题
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 的相反数是( )A、 B、 C、6 D、2. 如图的几何体是由一些小正方体组合而成的,这个几何体的左视图是( )
 A、
A、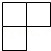 B、
B、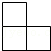 C、
C、 D、
D、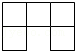 3. “一带一路”的“朋友圈”究竟有多大?“一带一路”涉及沿线65个国家,总涉及人口约4500000000,将4500000000用科学记数法表示为( )A、4.5×107 B、45×108 C、4.5×109 D、0.45×10104. 用四舍五入法把3.8963精确到百分位得到的近似数是( )A、3.89 B、3.900 C、3.9 D、3.905. 如图,直线 , 被直线所截,交点分别是点 , 点 , 则与是( )
3. “一带一路”的“朋友圈”究竟有多大?“一带一路”涉及沿线65个国家,总涉及人口约4500000000,将4500000000用科学记数法表示为( )A、4.5×107 B、45×108 C、4.5×109 D、0.45×10104. 用四舍五入法把3.8963精确到百分位得到的近似数是( )A、3.89 B、3.900 C、3.9 D、3.905. 如图,直线 , 被直线所截,交点分别是点 , 点 , 则与是( )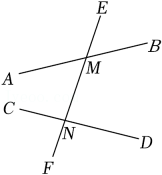 A、同位角 B、内错角 C、同旁内角 D、邻补角6. 下列多项式中,是二次三项式的是( )A、 B、 C、 D、7. 如图是某同学在体育课上跳远后留下的脚印,李老师在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A、同位角 B、内错角 C、同旁内角 D、邻补角6. 下列多项式中,是二次三项式的是( )A、 B、 C、 D、7. 如图是某同学在体育课上跳远后留下的脚印,李老师在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( ) A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、经过一点有且只有一条直线与已知直线垂直8. 如图, , 点在直线上,下列结论正确的是( )
A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、经过一点有且只有一条直线与已知直线垂直8. 如图, , 点在直线上,下列结论正确的是( )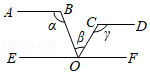 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题3分,共18分)
-
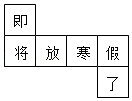
9. 单项式的系数是 .10. 两片棉田,一片有公顷,平均每公顷产棉花千克;另一片有公顷,平均每公顷产棉花千克,用代数式表示两片棉田上棉花的总产量为千克.11. 把多项式按y的升幂排列为 .12. 小华同学在一个正方体盒子的六个面上分别写了“即、将、放、寒、假、了”六个字,其平面展开图如图所示,请问在正方体盒子中,与“即”相对的面写的是字.
 13. 如图,点为中延长线上一点, , 若 , , 则 .
13. 如图,点为中延长线上一点, , 若 , , 则 .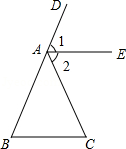 14. 如图,下列图形都是由大小相同的小正方形按一定的规律组成的,且每个小正方形的边长均为1,则第七个图形的周长是 .
14. 如图,下列图形都是由大小相同的小正方形按一定的规律组成的,且每个小正方形的边长均为1,则第七个图形的周长是 . …
…三、解答题(本大题共10小题,共78分)
-
15. 计算:16. 在如图所示的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点、、C均在格点上,只用无刻度的直尺,在给定的网格中按下述要求画图:
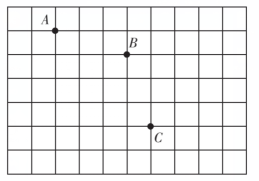 (1)、画射线;(2)、画直线;(3)、画线段 .17. 几何说理填空:
(1)、画射线;(2)、画直线;(3)、画线段 .17. 几何说理填空:如图,直线、相交于点 , 于点 , 平分 , 平分 , .
 (1)、;(2)、求的度数.(过程如下,补全过程)
(1)、;(2)、求的度数.(过程如下,补全过程)解:于点 ,
▲ ,
,
▲ ,
,
▲ ,
平分 ,
▲ = ▲ .
18. 如图,点、在线段上, , 点为的中点, . 求线段和的长.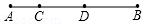 19. 先化简,再求值: ,其中 , .20. 某电业局要对市区的电线路进行检修,检修小组乘车从地出发,在东西向的马路上检修线路,晚上最后到达B地,如果规定向东行驶为正,向西行驶为负,检修车当天的行驶记录如下(单位:千米): , , , , , , , .(1)、B地在地的什么方向?距地多远?(2)、若检修车每千米耗油0.5升,当检修小组到达B地时,共耗油多少升?21. 如图,点A、B、C在同一条直线上,点D、E、G在同一条直线上,连结DB、CE,过点E作 , 已知 .
19. 先化简,再求值: ,其中 , .20. 某电业局要对市区的电线路进行检修,检修小组乘车从地出发,在东西向的马路上检修线路,晚上最后到达B地,如果规定向东行驶为正,向西行驶为负,检修车当天的行驶记录如下(单位:千米): , , , , , , , .(1)、B地在地的什么方向?距地多远?(2)、若检修车每千米耗油0.5升,当检修小组到达B地时,共耗油多少升?21. 如图,点A、B、C在同一条直线上,点D、E、G在同一条直线上,连结DB、CE,过点E作 , 已知 .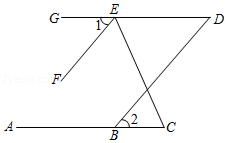 (1)、求证:∥;(2)、若平分 , 求的度数.22. 长春市“滴滴快车优享型”计价规则如下:车费由里程费和时长费两部分构成:
(1)、求证:∥;(2)、若平分 , 求的度数.22. 长春市“滴滴快车优享型”计价规则如下:车费由里程费和时长费两部分构成:里程费(分时段)
普通时段(除以下4个时段以外的时间)
2.20元公里
2.80元公里
2.75元公里
2.75元公里
2.80元公里
时长费(分时段)
普通时段(除以下2个时段以外的时间)
0.38元分钟
0.47元分钟
0.47元分钟
(1)、小刘同学在早上乘坐“滴滴快车优享型”去上学,行车里程6公里,行车时间10分钟,则他应付车费多少元?(2)、放学后小刘乘坐“滴滴快车优享型”回家,在学校上车,由于堵车,走另外一条路回家,平均速度是30公里小时,设走另外这条路的行车里程为公里 .①请问小刘应付车费多少元?(用含的代数式表示)
②当时,请计算小刘应付的车费.
23. 如图1, , 平分 , 点在射线上, , 垂足为点 , 平分 , 交射线于点 , 点是射线上一点,连结 .图1
 图2
图2 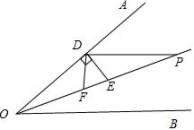 图3
图3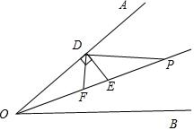 (1)、【探究一】如图1,若平分 , 则 .(2)、【探究二】如图2,若 , 求的度数.(3)、【探究三】如图3,若 , 则 .(4)、【探究四】若 , 直接写出的度数.24. 如图,已知数轴上有 , 两点,分别代表 , 20,两只电子蚂蚁甲,乙分别从 , 两点同时出发,甲沿线段以1个单位长度秒的速度向右运动,到达点处时运动停止;乙沿方向以4个单位长度秒的速度向左运动.
(1)、【探究一】如图1,若平分 , 则 .(2)、【探究二】如图2,若 , 求的度数.(3)、【探究三】如图3,若 , 则 .(4)、【探究四】若 , 直接写出的度数.24. 如图,已知数轴上有 , 两点,分别代表 , 20,两只电子蚂蚁甲,乙分别从 , 两点同时出发,甲沿线段以1个单位长度秒的速度向右运动,到达点处时运动停止;乙沿方向以4个单位长度秒的速度向左运动. (1)、 , 两点间的距离为个单位长度;乙到达点时共运动了秒.(2)、甲,乙在数轴上的哪个点相遇?(3)、多少秒时,甲、乙相距10个单位长度?(4)、若乙到达点后立刻掉头并保持速度不变,则甲到达点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
(1)、 , 两点间的距离为个单位长度;乙到达点时共运动了秒.(2)、甲,乙在数轴上的哪个点相遇?(3)、多少秒时,甲、乙相距10个单位长度?(4)、若乙到达点后立刻掉头并保持速度不变,则甲到达点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.