吉林省长春市绿园区2023-2024学年八年级上学期期末考试数学试题
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 在实数 , , 3.1415,中,无理数是( )A、 B、 C、3.1415 D、2. 27的立方根是( )A、9 B、 C、3 D、3. 计算的结果是( )A、 B、 C、 D、4. 若等腰三角形的两边长分别为2和5,则它的周长为( )A、9 B、7 C、12 D、9或125. 小东5分钟内共投篮60次,共进球15个,则小东进球的频率是( )A、0.25 B、60 C、0.26 D、156. 如图,在中,平分 , 若 , , 则( )
 A、 B、 C、 D、7. 在中, , . 用无刻度的直尺和圆规在内部作一个角 , 下列作法中不等于的是( )A、
A、 B、 C、 D、7. 在中, , . 用无刻度的直尺和圆规在内部作一个角 , 下列作法中不等于的是( )A、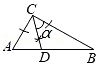 B、
B、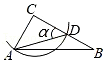 C、
C、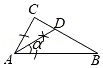 D、
D、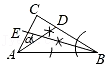 8. 如图1,2002年8月在北京召开的国际数学家大会会标原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成.如图2,如果大正方形的面积是16,直角三角形的直角边长分别为 , , 且 , 那么图中小正方形的面积是( )
8. 如图1,2002年8月在北京召开的国际数学家大会会标原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成.如图2,如果大正方形的面积是16,直角三角形的直角边长分别为 , , 且 , 那么图中小正方形的面积是( )图1
 图2
图2 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本大题共6小题,每小题3分,共18分)
-
9. 计算 的结果是.10. 分解因式: .11. 命题“同旁内角互补,两直线平行”的逆命题是 .12. 如图,在中, , 的垂直平分线交于点 , 交于点 . 已知的周长为 , 且 , 则的长为 .
 13. 如图,是直角三角形, , 分别以、为边向外作正方形.若图中两个正方形的面积和 , 则 .
13. 如图,是直角三角形, , 分别以、为边向外作正方形.若图中两个正方形的面积和 , 则 .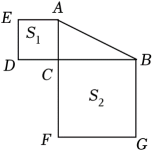 14. 如图,在中, , , 点是的中点,点在上,将沿折叠,若点的对应点恰好落在射线上,则与所夹锐角的度数是 .
14. 如图,在中, , , 点是的中点,点在上,将沿折叠,若点的对应点恰好落在射线上,则与所夹锐角的度数是 .
三、解答题(本大题共10小题,共78分)
-
15. 计算: .16. 计算: .17. 已知:如图, , , .
求证: .
 18. 先化简,再求值: , 其中 , .19. 若 , ,(1)、求的值;(2)、求的值.20. 学生的学业负担过重会严重影响学生对待学习的态度.为此某市教育部门对某学校的七年级学生对待学习的态度进行了一次调查(把学习态度分为三个层级,级:对学习很感兴趣;级:对学习较感兴趣;级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
18. 先化简,再求值: , 其中 , .19. 若 , ,(1)、求的值;(2)、求的值.20. 学生的学业负担过重会严重影响学生对待学习的态度.为此某市教育部门对某学校的七年级学生对待学习的态度进行了一次调查(把学习态度分为三个层级,级:对学习很感兴趣;级:对学习较感兴趣;级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题: (1)、此次调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中最小的扇形的圆心角的度数.21. 如图,有一张四边形纸片 , °.经测得 , , , .
(1)、此次调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中最小的扇形的圆心角的度数.21. 如图,有一张四边形纸片 , °.经测得 , , , . (1)、求、两点之间的距离.(2)、求这张纸片的面积.22. 图①、图②、图③均为的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,线段的端点、均为格点.分别在给定的网格中找一格点 , 按下列要求作图:
(1)、求、两点之间的距离.(2)、求这张纸片的面积.22. 图①、图②、图③均为的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,线段的端点、均为格点.分别在给定的网格中找一格点 , 按下列要求作图: (1)、在图①中,连结、 , 使 , ;(2)、在图②中,连结、 , 使 , ;(3)、在图③中,连结、 , 使 , .23. 如图
(1)、在图①中,连结、 , 使 , ;(2)、在图②中,连结、 , 使 , ;(3)、在图③中,连结、 , 使 , .23. 如图 (1)、【感知】如图①,是等边三角形,点是边上一点(点不与点、重合),作 , 使角的两边分别交边、于点、 , 且 . 若 , 则的大小是度;(2)、【探究】如图②,是等边三角形,点是边上一点(点不与点、重合),作 , 使角的两边分别交边、于点、 , 且 . 求证:;(3)、【应用】如图③,是等边三角形, , 点是边的中点,作 , 使角的两边分别交边、于点、 , 且 . 则四边形的周长为 .24. 如图,在长方形中, , . 延长到点 , 使 , 连结 . 动点从点出发,沿以每秒1个单位的速度向终点运动,设点运动的时间为(秒).
(1)、【感知】如图①,是等边三角形,点是边上一点(点不与点、重合),作 , 使角的两边分别交边、于点、 , 且 . 若 , 则的大小是度;(2)、【探究】如图②,是等边三角形,点是边上一点(点不与点、重合),作 , 使角的两边分别交边、于点、 , 且 . 求证:;(3)、【应用】如图③,是等边三角形, , 点是边的中点,作 , 使角的两边分别交边、于点、 , 且 . 则四边形的周长为 .24. 如图,在长方形中, , . 延长到点 , 使 , 连结 . 动点从点出发,沿以每秒1个单位的速度向终点运动,设点运动的时间为(秒). (1)、的长为 .(2)、连结 , 当时,求的值.(3)、连结 .
(1)、的长为 .(2)、连结 , 当时,求的值.(3)、连结 .①当是直角三角形时,求的值.
②当是等腰三角形时,直接写出的值.