吉林省长春市德惠四中、五中、二十九中2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题：本题共6小题，每小题2分，共12分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 计算 $(- \frac{5}{13})^{3} \times (- \frac{13}{5})^{2}$ 所得结果为（）

A、 $1$ B、 $- 1$ C、 $- \frac{5}{13}$ D、 $- \frac{13}{5}$

查看试题解析
3. 平面直角坐标系中，点P（-2，3）关于x轴对称的点的坐标为（　　）

A、（-2，-3） B、（2，-3） C、（-3，-2） D、（3，-2）

查看试题解析
4. 如图，在 $△ A B C$ 中，点 $D$ 、 $E$ 分别在 $A B$ 、 $A C$ 边上， $D E / / B C$ ，点 $F$ 在 $B C$ 的延长线上，若 $∠ A C F = 140 °$ ， $∠ A D E = 105 °$ ，则 $∠ A$ 的大小为（）

A、 $30 °$ B、 $35 °$ C、 $50 °$ D、 $75 °$

查看试题解析
5. 如图，用直尺和圆规作已知角的平分线的示意图，则说明∠CAD＝∠DAB的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
6. 某书店分别用 $600$ 元和 $900$ 元两次购进该小说，第二次数量比第一次多 $50$ 套，且两次进价相同 $.$ 若设该书店第一次该小说购进 $x$ 套，由题意列方程正确的是（）

A、 $\frac{600}{x} = \frac{900}{x - 50}$ B、 $\frac{600}{x - 50} = \frac{900}{x}$ C、 $\frac{600}{x} = \frac{900}{x + 50}$ D、 $\frac{600}{x + 50} = \frac{900}{x}$

查看试题解析

二、填空题：本题共8小题，每小题3分，共24分。

7. 计算： $(2 a^{2} b^{3})^{2} =$ ．

查看试题解析
8. 在代数式 $\frac{5}{3 a}$ ， $\frac{7}{10}$ ， $\frac{2}{2 b - 1}$ ， $\frac{y - 1}{2}$ ， $x + \frac{y}{8}$ 中，是分式的有个．

查看试题解析
9. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 60 °$ ， $B C = 4 c m$ ，则 $A B =$ $c m$ ．

查看试题解析
10. 如图， $A C = A D$ ， $B C = B D$ ，则 $△ A B C$ ≌ $△ A B D$ ，应用的判定方法是．

查看试题解析
11. 若a-2b=3，则2a-4b-5=.

查看试题解析
12. 如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm，则AB=cm.

查看试题解析
13. 如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5= ．

查看试题解析
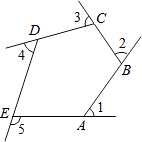14. 某同学上学时步行，回家时乘车，路上共用 $a$ 小时 $.$ 如果往返都乘车，则共需 $b$ 小时，那么往返都步行需要小时．

查看试题解析

三、计算题：本大题共1小题，共5分。

15. 长春市绿园区环卫处在西安大路清扫上安排了A、B两辆清扫车．A车比B车每小时多清扫路面6km，若A车清扫路面42km与B车清扫路面 3 5km所用的时间相同，求B车每小时清扫路面的长度．

查看试题解析

四、解答题：本题共11小题，共79分。解答应写出文字说明，证明过程或演算步骤。

16. 计算： $(x + 2 y) (x - 2 y) - y (3 - 4 y)$ ．

查看试题解析
17. 解方程： $\frac{2}{3} + \frac{x}{3 x - 1} = \frac{1}{9 x - 3}$ .

查看试题解析
18. 如图，在3×3的正方形网格中，有格点△ABC和△DEF，且△ABC和△DEF关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的△DEF及其对称轴MN．

查看试题解析
19. 已知：如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C．
求证：∠A=∠D．

查看试题解析
20. 先化简： $(\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ，然后解答下列问题：

(1)、当 $x = 3$ 时，求原代数式的值；

(2)、原代数式的值能等于 $- 1$ 吗？为什么？

查看试题解析
21. 在平面直角坐标系中， $△ A B C$ 的三个顶点的位置如图所示．

(1)、请画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A' B' C'$ ； $($ 其中 $A'$ ， $B'$ ， $C'$ 分别是 $A$ ， $B$ ， $C$ 的对应点，不写画法 $)$

(2)、直接写出 $A'$ ， $B'$ ， $C'$ 点的坐标．

查看试题解析
22. 如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．
示例：
即 $4 + 3 = 7$ ，
则：

(1)、用含 $x$ 的式子表示 $m =$ ；

(2)、当 $y = - 2$ 时， $n$ 的值为．

查看试题解析
23. 一个等腰三角形的周长为28cm.

(1)、如果底边长是腰长的1.5倍，求这个等腰三角形的三边长；

(2)、如果一边长为10cm，求这个等腰三角形的另两边长.

查看试题解析
24. 下面是某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行因式分解的过程．
解：设 $x^{2} - 4 x = y$ ，
原式 $= (y + 2) (y + 6) + 4 ($ 第一步 $)$
$= y^{2} + 8 y + 16 ($ 第二步 $)$
$= (y + 4)^{2} ($ 第三步 $)$
$= (x^{2} - 4 x + 4)^{2} ($ 第四步 $)$

(1)、该同学第二步到第三步运用了因式分解的____；

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学因式分解的结果是否彻底？若不彻底，请直接写出因式分解的最后结果；

(3)、请你模仿以上方法尝试对多项式 $(x^{2} - 2 x) (x^{2} - 2 x + 2) + 1$ 进行因式分解．

查看试题解析
25. 小明去离家 $2.4$ 千米的体育馆看球赛，进场时，发现门票还放在家中，此时离比赛开始还有 $45$ 分钟，于是他立即步行 $($ 匀速 $)$ 回家取票．在家取票用时 $2$ 分钟，取到票后，他马上骑自行车 $($ 匀速 $)$ 赶往体育馆．已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少 $20$ 分钟，骑自行车的速度是步行速度的 $3$ 倍．

(1)、小明步行的速度 $($ 单位：米 $/$ 分钟 $)$ 是多少？

(2)、小明能否在球赛开始前赶到体育馆？

查看试题解析
26. 在 $△ A B C$ 中， $A B = A C \neq B C$ ，点 $D$ 和点 $A$ 在直线 $B C$ 的同侧， $B D = B C$ ， $∠ B A C = α$ ， $∠ D B C = β$ ，且 $α + β = 120 °$ ，连接 $A D$ ，求 $∠ A D B$ 的度数 $. ($ 不必解答 $)$

(1)、小聪先从特殊问题开始研究，当 $α = 90 °$ ， $β = 30 °$ 时，利用轴对称知识，以 $A B$ 为对称轴构造 $△ A B D$ 的轴对称图形 $△ A B D'$ ，连接 $C D' ($ 如图 $2)$ ，然后利用 $α = 90 °$ ， $β = 30 °$ 以及等边三角形等相关知识便可解决这个问题 $.$ 请结合小聪研究问题的过程和思路，在这种特殊情况下填空：
$△ D' B C$ 的形状是三角形， $∠ A D B$ 的度数为；

(2)、在原问题中，当 $∠ D B C < ∠ A B C ($ 如图 $1)$ 时，请计算 $∠ A D B$ 的度数；

(3)、在 $(2)$ 中，若 $B C = 6$ ， $A D = 2 .$ 请直接写出 $△ A B D$ 的面积．

查看试题解析