贵州省贵阳市2023-2024学年九年级上学期质量联考期末数学试卷

试卷更新日期：2024-02-01 类型：期末考试

进入出卷网下载

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请在答题卡

1. 下列关于x的方程中，一定是一元二次方程的是（　　）

A、3x+2＝0 B、x²﹣3x＝0 C、x+3xy﹣1＝0 D、 $\frac{1}{x} - 4 = 0$

查看试题解析
2. 这是一个水平放置的木陀螺（上面是圆柱体，下面是圆锥体）玩具，它的主视图（　　）

A、 B、 C、 D、

查看试题解析
3. 如图，把△AOB缩小后得到△COD ，则△COD与△AOB的相似比为（　　）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析
4. 一个口袋中装有黑球、白球共15个，这些球除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有60次摸到黑球，请估计口袋中黑球的个数大约有（　　）

A、3个 B、5个 C、6个 D、9个

查看试题解析
5. 已知菱形的边长为13cm ，它的一条对角线长为10cm ，则该菱形的面积为（　　）

A、60cm² B、120cm² C、240cm² D、480cm²

查看试题解析
6. 若x＝﹣1是关于x的一元二次方程2x²﹣3mx+1＝0的一个根，则m的值为（　　）

A、﹣1 B、1 C、0 D、无法确定

查看试题解析
7. 若点A（﹣1，a），B（b ， 1），C（2，c）在反比例函数 $y = - \frac{1}{x}$ 的图象上，则a ， b ， c的大小关系是（　　）

A、c＞b＞a B、b＞a＞c C、a＞c＞b D、b＞c＞a

查看试题解析
8. 如图，将长方形纸片ABCD折叠，使点D与点B重合，点C落在点 $C^{'}$ 处，折痕为EF，若∠ABE＝30°，则 $∠ E F C^{'}$ 的度数为（）

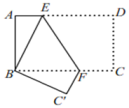A、120° B、100° C、150° D、90°

查看试题解析
9. 若关于x的方程ax²﹣3x+c＝0有两个不相等的实数根，则下列选项中，满足条件的实数a ， c的值可以是（　　）

A、a＝1，c＝3 B、a＝﹣2，c＝﹣4 C、a＝﹣1，c＝3 D、a＝5，c＝1

查看试题解析
10. 如图，矩形ABCD中，对角线AC、BD相交于点O ，过点O作OE⊥BD交AD于点E ，已知AB＝5，△DOE的面积为 $\frac{15}{2}$ ，则DE的长为（　　）

A、5 B、6 C、7 D、 $5 \sqrt{2}$

查看试题解析
11. 如图，在平面直角坐标系中，点O为坐标原点，平行四边形ABOD的顶点B在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，顶点A在反比例函数 $y = - \frac{2}{x}$ 的图象上，顶点D在x轴的负半轴上．若平行四边形ABOD的面积是5，则k的值是（　　）

A、3 B、4 C、2 D、1

查看试题解析
12. 如图，在正方形ABCD和CEFG中，连接AF交CD于点H ， AB＝6，DH＝3GH ， I是AF的中点，那么CI的长是（　　）

A、 $2 \sqrt{5}$ B、2 C、 $3 \sqrt{5}$ D、3

查看试题解析

二、填空题（每小题4分，共16分）

13. 一元二次方程x²﹣49＝0的根是．

查看试题解析
14. 如图，AB∥CD ， AD与BC相交于点O ．若 $\frac{B O}{O C} = \frac{2}{3}$ ， AD＝15，则AO的长为．

查看试题解析
15. 调查显示，某商场一款小型电器的销售量是售价的反比例函数，（调查获得的部分数据如下表）．
售价x（元/台）
200
250
400
500
销售量y（台）
40
32
20
16
已知该小型电器的进价为180元/台，要使该小型电器每天的销售利润达到3500元，其售价应定为元．

查看试题解析
16. 阅读理解：平面内任意两点（x₁ ， y₁），（x₂ ， y₂）的距离可以表示为 $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ，反之， $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ 表示点（x₁ ， y₁）与点（x₂ ， y₂）之间的距离．尝试利用阅读内容解决问题：如图，在正方形ABCD中，M为AD上一点，且 $\frac{A M}{M D} = \frac{3}{1}$ ， E ， F分别为BC ， CD上的动点，且BE＝2DF ，若AB＝4，则ME+2AF的最小值是．

查看试题解析

三、解答题（本大题共9题，共98分.解答应写出必要的文字说明、证明过程或演算步骤）

17. 用适当的方法解下列方程：

(1)、x（x﹣5）＝3x﹣15；

(2)、2y²﹣9y+5＝0．

查看试题解析
18. 如图，学习完投影后，小光同学在灯光下观察自己的影子．线段AB表示小光站立的位置，线段CD表示此时操场上的灯杆，点C为路灯所在位置．

(1)、画出小光在路灯C照明下的投影示意图，并记作BE；

(2)、如果小光身高1.8m ，他站在距离灯杆CD为5m的B处时，测得自己的影长BE＝3m ，求灯杆CD的高度．

查看试题解析
19. 为了锻炼身体，增强体质，某校将举行一年一度的校际运动会．体育组想了解同学们最喜爱的体育项目，由此设计了一份调查问卷．问卷要求每人必选且只能选一种最喜爱的体育项目．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中信息解答下列问题：

(1)、这次共调查了人；

(2)、在扇形统计图中，表示“铅球”的扇形圆心角是多少度？

(3)、小李和小文都想从“跳高”、“短跑”、“铅球”中任选一种项目进行比赛，请用画树状图或列表的方法，求两人恰好选择同一种比赛项目的概率．

查看试题解析
20. 如图，在△ABC中，BM平分∠ABC ， MB＝MC ．

(1)、求证：△AMB∽△ABC；

(2)、若AM＝3，MB＝6，求AB的长．

查看试题解析
21. 如图，已知在平行四边形ABCD中，AE平分∠BAD交BC于点E ，点F在AD上，AF＝AB ，连接BF交AE于点O ，连接EF ．

(1)、求证：四边形ABEF是菱形；

(2)、若BF＝8，AB＝5，求AE的长．

查看试题解析
22. 如图，一块长为28m、宽为20m的长方形土地，在上面修筑了同样宽的三条道路（图中阴影部分），空白的部分种上各种花草．要使种花草的土地面积为416m² ，你能求出道路的宽吗？

查看试题解析
23. 在学习了光的反射定律后，数学综合实践小组想利用光的反射定律（反射角等于入射角）测量池塘对岸一棵树的高度AB ，测量步骤如下：
①如图，在地面上的点E处放置一块平面镜（镜子大小忽略不计），小阳站在BE的延长线上，当小阳从平面镜中刚好看到树的顶点A时，测得小阳到平面镜的距离DE＝2m ，小阳的眼睛点C到地面的距离CD＝1.6m；
②将平面镜从点E沿BE的延长线移动6m放置到点H处，小阳从点D处移动到点G ，此时小阳的眼睛点F又刚好在平面镜中看到树的顶点A ，这时测得小阳到平面镜的距离GH＝3.2m ．请根据以上测量过程及数据求出树的高度AB ．

查看试题解析
24. 在平面直角坐标系中，一次函数y＝ax+b（a≠0）的图象与反比例函数 $y = \frac{k}{x}$ （k＜0）的图象交于第二、四象限内的A ， B两点，与x轴交于C点，过点A作AD⊥y轴，垂足为点D ， OD＝3， $\frac{A D}{O D} = \frac{4}{3}$ ，点B的坐标为（c ， ﹣2）．

(1)、求该反比例函数和一次函数的表达式；

(2)、根据图象直接写出使ax+b＜ $\frac{k}{x}$ 成立的x的取值范围；

(3)、形如x²﹣a＞0（a为常数，a＞0）的解集为：x＞ $\sqrt{a}$ 或x＜﹣ $\sqrt{a}$ ，过点M（6，0）作垂直于x轴的直线MN ，直线y＝x+n与双曲线y＝ $\frac{k}{x}$ （k＜0）交于点P（x₁ ， y₁），Q（x₂ ， y₂），与直线MN交于点R（x₃ ， y₃），若y₁＜y₂＜y₃时，求n的取值范围．

查看试题解析
25. 如图①，在正方形ABCD中，点E ， F分别在边AB、BC上，DF⊥CE于点O ，点G ， H分别在边AD、BC上，GH⊥CE ．

(1)、问题解决：①写出DF与CE的数量关系：；
② $\frac{G H}{C E}$ 的值为；

(2)、类比探究，如图②，在矩形ABCD中， $\frac{A B}{B C} = k$ （k为常数），将矩形ABCD沿GH折叠，使点C落在AB边上的点E处，得到四边形EFGH交AD于点P ，连接CE交GH于点O ．试探究GH与CE之间的数量关系，并说明理由；

(3)、拓展应用，如图③，四边形ABCD中，∠BAD＝90°，AB＝BC＝6，AD＝CD＝4，BF⊥CE ，点E、F分别在边AB、AD上，求 $\frac{C E}{B F}$ 的值．

查看试题解析

售价x（元/台）	200	250	400	500
销售量y（台）	40	32	20	16