贵州省贵阳市三联教育集团2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
-
1. “力箭一号”(ZK﹣1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,首次飞行任务取得圆满成功.把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线2. 如图,数轴上点A和点B分别表示数a和b , 则下列式子正确的是( )
 A、a>0 B、ab<0 C、a﹣b>0 D、a+b>03. 第19届亚运会于2023年9月23日在浙江省杭州市开幕,参加赛事的运动员共有12417人.12417用科学记数法表示为( )A、0.12417×105 B、0.12417×10﹣5 C、1.2417×104 D、1.2417×10﹣44. 检测4个排球的重量,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )A、+1 B、+0.5 C、﹣0.4 D、﹣1.25. 下列各式运算正确的是( )A、2(a+3b)=2a+3b B、﹣(a﹣b)=﹣a﹣b C、2a2b﹣2ab2=0 D、3ab﹣3ba=06. 下列说法中,错误的是( )A、两点之间的所有连线中,线段最短 B、经过两点的直线有且只有一条 C、连接两点的线段叫做两点间的距离 D、线段MN和线段NM是同一条线段7. 如图,表中给出的是某月的月历,任意选取“凹”型框中的5个数(如阴影部分所示).请你运用所学的数学知识来研究,这5个数的和不可能是( )
A、a>0 B、ab<0 C、a﹣b>0 D、a+b>03. 第19届亚运会于2023年9月23日在浙江省杭州市开幕,参加赛事的运动员共有12417人.12417用科学记数法表示为( )A、0.12417×105 B、0.12417×10﹣5 C、1.2417×104 D、1.2417×10﹣44. 检测4个排球的重量,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )A、+1 B、+0.5 C、﹣0.4 D、﹣1.25. 下列各式运算正确的是( )A、2(a+3b)=2a+3b B、﹣(a﹣b)=﹣a﹣b C、2a2b﹣2ab2=0 D、3ab﹣3ba=06. 下列说法中,错误的是( )A、两点之间的所有连线中,线段最短 B、经过两点的直线有且只有一条 C、连接两点的线段叫做两点间的距离 D、线段MN和线段NM是同一条线段7. 如图,表中给出的是某月的月历,任意选取“凹”型框中的5个数(如阴影部分所示).请你运用所学的数学知识来研究,这5个数的和不可能是( ) A、31 B、56 C、67 D、1268. 已知等式a=b , 则下列变形错误的是( )A、|a|=|b| B、 C、a2=b2 D、2a﹣2b=09. 如图是一个几何体的平面展开图,则这个几何体是( )
A、31 B、56 C、67 D、1268. 已知等式a=b , 则下列变形错误的是( )A、|a|=|b| B、 C、a2=b2 D、2a﹣2b=09. 如图是一个几何体的平面展开图,则这个几何体是( )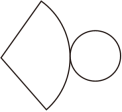 A、
A、 B、
B、 C、
C、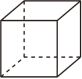 D、
D、 10. 为了了解2015年我县九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩,下列说法正确的是( )A、2015年我县九年级学生是总体 B、样本容量是1000 C、1000名九年级学生是总体的一个样本 D、每一名九年级学生是个体11. 如图所示是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年教育费用判断正确的是( )
10. 为了了解2015年我县九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩,下列说法正确的是( )A、2015年我县九年级学生是总体 B、样本容量是1000 C、1000名九年级学生是总体的一个样本 D、每一名九年级学生是个体11. 如图所示是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年教育费用判断正确的是( )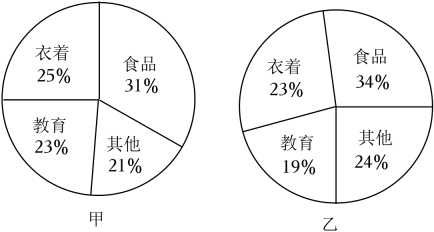 A、甲户比乙户多 B、乙户比甲户多 C、甲、乙两户一样多 D、无法确定哪一户多12. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方﹣九宫格,把1﹣9这9个数填入3×3方格中,使每一横行,每一竖列以及两条斜对角线上的数之和都相等.如图是一个未完成的“幻方”,则其中x的值是( )
A、甲户比乙户多 B、乙户比甲户多 C、甲、乙两户一样多 D、无法确定哪一户多12. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方﹣九宫格,把1﹣9这9个数填入3×3方格中,使每一横行,每一竖列以及两条斜对角线上的数之和都相等.如图是一个未完成的“幻方”,则其中x的值是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(本大题共4小题,每小题4分,共16分)
-
13. ﹣3 的倒数是.14. 单项式的系数是 .15. 将长方形纸片对折1次可得1条折痕,对折2次可得3条折痕,对折3次可得7条折痕,那么对折6次可得 条折痕.
 16. 在直线l上顺次取A , B , C三点,使得AB=5cm , BC=7cm . 如果点O是线段AC的中点,那么线段OB的长度是 cm .
16. 在直线l上顺次取A , B , C三点,使得AB=5cm , BC=7cm . 如果点O是线段AC的中点,那么线段OB的长度是 cm .三、解答题(本大题共9题,各题分值见题后,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 计算:(1)、﹣3+(﹣2)×5﹣(﹣3);(2)、﹣12023+[(﹣5)2﹣3]÷|﹣2|.18. 解方程:(1)、3x﹣1=x+7;(2)、 .19. 如图是由一些相同的小正方体组成的几何体.
 (1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加 个小正方体.20. 已知代数式A=6x2+3xy+2y , B=3x2﹣2xy+5x .(1)、求A﹣2B;(2)、当 , y=﹣6时,求A﹣2B的值;(3)、若A﹣2B的值与x的取值无关,求y的值.21. 如图,已知OC是∠AOB内部任意的一条射线,OM、ON分别是∠AOC、∠BOC的平分线.
(1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加 个小正方体.20. 已知代数式A=6x2+3xy+2y , B=3x2﹣2xy+5x .(1)、求A﹣2B;(2)、当 , y=﹣6时,求A﹣2B的值;(3)、若A﹣2B的值与x的取值无关,求y的值.21. 如图,已知OC是∠AOB内部任意的一条射线,OM、ON分别是∠AOC、∠BOC的平分线. (1)、若∠AOM=25°,∠BON=35°,求∠MON的度数;(2)、若∠AOB=β,求∠MON的度数.22. 某检修站,工人乘一辆汽车沿东西方向的公路检修线路,约定向东为正,向西为负,从A地出发到收工时,行走记录为(单位:千米):
(1)、若∠AOM=25°,∠BON=35°,求∠MON的度数;(2)、若∠AOB=β,求∠MON的度数.22. 某检修站,工人乘一辆汽车沿东西方向的公路检修线路,约定向东为正,向西为负,从A地出发到收工时,行走记录为(单位:千米):+15,﹣2,+5,﹣1,+10,﹣3,﹣2,﹣12,+4,﹣5,+6
(1)、计算收工时,工人在A地的哪一边,距A地多远?(2)、若汽车每行驶100千米耗油8升,求这一天汽车共耗油多少升?23. 一商店在某一时间以每件a元(a>0)的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%.(1)、当a=60时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?(2)、小安发现:不论a为何值,这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确?24. 为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了m名学生,将一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如下的统计图和统计表:
等级
次数
频数
不合格
100≤x<120
4
合格
120≤x<140
a
良好
140≤x<160
12
优秀
160≤x<180
10
请结合上述信息完成下列问题:
(1)、m= , a=;(2)、请补全频数分布直方图;(3)、在扇形统计图中,“良好”等级对应的圆心角的度数是 ;(4)、若该校有1600名学生,根据抽样调查结果,请估计该校有多少名学生一分钟跳绳次数达到合格及以上.25. 已知:如图数轴上有A、B、C三点,点A和点B间距20个单位长度且点A、B表示的有理数互为相反数,AC=40,数轴上有一动点P从点A出发,以2个单位/秒的速度向右沿数轴运动,设运动时间为t秒(t>0). (1)、点A表示的有理数是 , 点C表示的有理数是 , 点P表示的数是 (用含t的式子表示).(2)、当t=秒时,P、B两点之间相距8个单位长度?(3)、若点A、点B和点C与点P同时在数轴上运动,点A以1个单位/秒的速度向左运动,点B和点C分别以3个单位/秒和4个单位/秒的速度向右运动,是否存在常数m , 使得mAP+7BP﹣2CP为一个定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
(1)、点A表示的有理数是 , 点C表示的有理数是 , 点P表示的数是 (用含t的式子表示).(2)、当t=秒时,P、B两点之间相距8个单位长度?(3)、若点A、点B和点C与点P同时在数轴上运动,点A以1个单位/秒的速度向左运动,点B和点C分别以3个单位/秒和4个单位/秒的速度向右运动,是否存在常数m , 使得mAP+7BP﹣2CP为一个定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.