贵州省铜仁市江口县2023-2024学年八年级上学期期末数学模拟试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(共10小题,满分40分,每小题4分)
-
1. 在实数:0, , , , 0.020020002…(每两个2之间零的个数依次增加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算正确的是( )A、20230=1 B、 C、2﹣1=﹣2 D、(x+1)2=x2+13. 已知三角形两边长分别为5cm和16cm , 则下列线段中能作为该三角形第三边的是( )A、24cm B、15cm C、11cm D、8cm4. 若9的整数部分为a , 小数部分为b , 则2a+b等于( )A、12 B、13 C、14 D、155. 下列不等式变形正确的是( )A、由a>b , 得ac>bc B、由a>b , 得a﹣2<b﹣2 C、由ab>ac , 得b>c D、由 , 得b>c6. 如图,在△ABC中,AB=AC , DB=BC , ∠B=70°,∠ACD的度数为( )
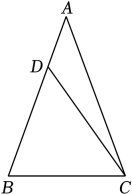 A、10° B、15° C、25° D、30°7. 如图,用尺规作图作 的平分线 ,第一步是以 为圆心,任意长为半径画弧,分别交 于点 ;第二步是分别以 为圆心,以大于 长为半径画弧,两圆弧交于 点,连接 ,那么 为所作,则说明 的依据是( )
A、10° B、15° C、25° D、30°7. 如图,用尺规作图作 的平分线 ,第一步是以 为圆心,任意长为半径画弧,分别交 于点 ;第二步是分别以 为圆心,以大于 长为半径画弧,两圆弧交于 点,连接 ,那么 为所作,则说明 的依据是( )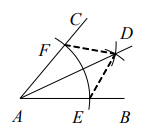 A、 B、 C、 D、8. 如图,AB与CD相交于点O , AC∥BD , 只添加一个条件,能判定△ACO≌△BDO的是( )
A、 B、 C、 D、8. 如图,AB与CD相交于点O , AC∥BD , 只添加一个条件,能判定△ACO≌△BDO的是( ) A、∠A=∠D B、AO=BO C、AC=OB D、AB=CD9. 某中学在校内劳动基地开展了一堂特殊的劳动课,计划九(1)班共采摘100千克蔬菜,在实际采摘之前将班级10名同学调往其他劳动区域,这样剩余同学实际平均每人需要采摘的重量是原计划全班学生平均每人需要采摘重量的倍,设九(1)班学生的人数为x名,则下列方程正确的是( )A、 B、 C、 D、10. 如图,正五边形中,F为边中点,连接 , 则的度数是( )
A、∠A=∠D B、AO=BO C、AC=OB D、AB=CD9. 某中学在校内劳动基地开展了一堂特殊的劳动课,计划九(1)班共采摘100千克蔬菜,在实际采摘之前将班级10名同学调往其他劳动区域,这样剩余同学实际平均每人需要采摘的重量是原计划全班学生平均每人需要采摘重量的倍,设九(1)班学生的人数为x名,则下列方程正确的是( )A、 B、 C、 D、10. 如图,正五边形中,F为边中点,连接 , 则的度数是( )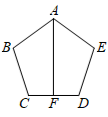 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,满分24分,每小题4分)
-
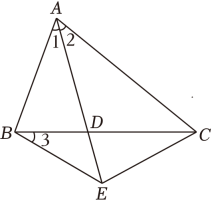
11. 计算:9 .12. 若分式的值为0,则m的值为 .13. 写出命题“等边三角形是等腰三角形”的逆命题 .14. 若关于x的方程0产生增根,则m= .15. 已知正数x的两个平方根是2m﹣3和3m﹣17,则m= .16. 如图,在△ABC中,D为边BC上一点,延长AD至点E , 连接BE , CE , ∠ABD∠3=90°,∠1=∠2=∠3,有以下几个结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE . 其中正确的结论是 (填序号).
三、解答题(共5小题,满分48分)
-
17. 解分式方程:1.18. 先化简,再求值: , 其中x=﹣5.19. 解不等式组: .20. 如图,AD,BC相交于点O,AC=BD,∠C=∠D=90°.
 (1)、求证:OA=OB;(2)、若∠ABC=30°,OC=4,求BC的长.21. 已知:如图,△ABC和△CDE均为等腰三角形,AC=BC,EC=DC,BD⊥AD于点D,AD交BC于点F,点A、E、D三点共线,连接BD.
(1)、求证:OA=OB;(2)、若∠ABC=30°,OC=4,求BC的长.21. 已知:如图,△ABC和△CDE均为等腰三角形,AC=BC,EC=DC,BD⊥AD于点D,AD交BC于点F,点A、E、D三点共线,连接BD.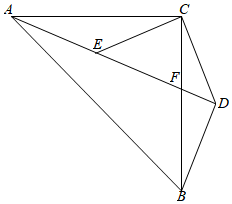 (1)、若∠ACE=∠BCD,AD=8,BD= AD,求DE的长;(2)、若∠ACB=∠ECD=90°,且BD=CE,求证:BC=AB﹣CF.
(1)、若∠ACE=∠BCD,AD=8,BD= AD,求DE的长;(2)、若∠ACB=∠ECD=90°,且BD=CE,求证:BC=AB﹣CF.四、解答题(共1小题,满分12分,每小题12分)
-
22. 阅读下列解题过程:
; .
请回答下列问题:
(1)、观察上面的解题过程,化简:; .(2)、利用上面提供的解法,请化简: .五、解答题(共1小题,满分12分,每小题12分)
-
23. 某校教师前往距离学校10千米的党史学习教育基地参观学习,一部分教师骑自行车先走,过了20分钟后,其余教师乘汽车出发,结果他们同时到达,已知汽车的速度是骑车教师速度的3倍,求骑车教师的速度.
六、解答题(共1小题,满分14分,每小题14分)
-
24. 如图所示,已知△ABC中,AB=AC=12厘米,BC=10厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒由B出发向C点运动,同时点Q在线段CA上以4厘米/秒由点A出发向C点运动.设运动时间为t秒.
 (1)、用含t的式子表示第t秒时,BP=厘米,CQ=厘米.(2)、如果点P与点Q分别从B , A两点同时出发,经过2秒后,△BPD与△CPQ是否全等?请说明理由.(3)、如果点P与点Q分别从B , A两点同时出发,经过几秒后,△CPQ是以PQ为底的等腰三角形?
(1)、用含t的式子表示第t秒时,BP=厘米,CQ=厘米.(2)、如果点P与点Q分别从B , A两点同时出发,经过2秒后,△BPD与△CPQ是否全等?请说明理由.(3)、如果点P与点Q分别从B , A两点同时出发,经过几秒后,△CPQ是以PQ为底的等腰三角形?
-
-