贵州省毕节市七星关区2023-2024学年七年级上学期期末数学模拟试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(共12小题,满分48分,每小题4分)
-
1. 以下四个选项分别表示某市今年四个月的平均气温,其中平均气温最低的是( )A、﹣3℃ B、15℃ C、﹣10℃ D、2℃2. 围成下列立体图形的各个面中,每个面都是平的是( )A、
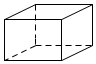 长方体
B、
长方体
B、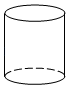 圆柱体
C、
圆柱体
C、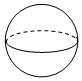 球体
D、
球体
D、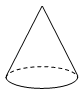 圆锥体
3. 已知一个单项式的系数是2,次数是3,则这个单项式可以是( )A、3x2 B、 C、2x3y D、2x34. 北京2022年冬奥会标志性场馆“冰丝带”——国家速滑馆,于2021年4月30日完成首次全冰面制冰,冰面面积约12000平方米,是目前亚洲最大的冰面,用科学记数法可以把数字12000表示为( )A、0.12×105 B、1.2×104 C、1.2×105 D、12×1035. 下列调查中,适合用全面调查方式的是( )A、了解某班学生的身高情况 B、了解一批灯泡的使用寿命 C、了解目前中学生的睡眠情况 D、了解一批炮弹的杀伤半径6. 如果3m=3n , 那么下列等式不一定成立的是( )A、m﹣3=n﹣3 B、2m+3=3n+2 C、5+m=5+n D、7. 数轴上有四个点分别表示的是1,3,﹣2,0,其中最左边的点表示的数是( )A、3 B、1 C、0 D、﹣28. 如图, 在 的内部,且 ,若 的度数是一个正整数,则图中所有角的度数之和可能是( )
圆锥体
3. 已知一个单项式的系数是2,次数是3,则这个单项式可以是( )A、3x2 B、 C、2x3y D、2x34. 北京2022年冬奥会标志性场馆“冰丝带”——国家速滑馆,于2021年4月30日完成首次全冰面制冰,冰面面积约12000平方米,是目前亚洲最大的冰面,用科学记数法可以把数字12000表示为( )A、0.12×105 B、1.2×104 C、1.2×105 D、12×1035. 下列调查中,适合用全面调查方式的是( )A、了解某班学生的身高情况 B、了解一批灯泡的使用寿命 C、了解目前中学生的睡眠情况 D、了解一批炮弹的杀伤半径6. 如果3m=3n , 那么下列等式不一定成立的是( )A、m﹣3=n﹣3 B、2m+3=3n+2 C、5+m=5+n D、7. 数轴上有四个点分别表示的是1,3,﹣2,0,其中最左边的点表示的数是( )A、3 B、1 C、0 D、﹣28. 如图, 在 的内部,且 ,若 的度数是一个正整数,则图中所有角的度数之和可能是( ) A、340° B、350° C、360° D、370°9. 随着互联网的高速发展,“微商”经营已成为大众创业新途径,某微信平台上一种商品标价为240元,按标价的80%出售,仍可获利20%,设该商品进价是x元,则所列方程是( )A、240×80%﹣x=20%x B、240×80%﹣x=20% C、240×80%﹣x=240×20% D、240﹣80%x=240×20%10. 下列说法正确的是( )A、平角的度数是360° B、用两个钉子把木条固定在墙上,数学原理是“两点之间,线段最短” C、已知线段AB=2cm , 延长线段AB到C , 使BC=6cm , 则AC=8cm D、过某个多边形一个顶点的所有对角线,将这个多边形分成6个三角形,则这个多边形是六边形11. 如图,若AC=48,M为AC的中点,ABAC , 则BM的长度为( )
A、340° B、350° C、360° D、370°9. 随着互联网的高速发展,“微商”经营已成为大众创业新途径,某微信平台上一种商品标价为240元,按标价的80%出售,仍可获利20%,设该商品进价是x元,则所列方程是( )A、240×80%﹣x=20%x B、240×80%﹣x=20% C、240×80%﹣x=240×20% D、240﹣80%x=240×20%10. 下列说法正确的是( )A、平角的度数是360° B、用两个钉子把木条固定在墙上,数学原理是“两点之间,线段最短” C、已知线段AB=2cm , 延长线段AB到C , 使BC=6cm , 则AC=8cm D、过某个多边形一个顶点的所有对角线,将这个多边形分成6个三角形,则这个多边形是六边形11. 如图,若AC=48,M为AC的中点,ABAC , 则BM的长度为( ) A、10 B、9.5 C、9 D、812. 如图图形都是由形状、大小完全相同的“●”按一定规律所组成,其中图①共有6个黑点,图②共有9个黑点,图③共有12个黑点…,按此规律排列,则图⑦中黑点的个数为( )
A、10 B、9.5 C、9 D、812. 如图图形都是由形状、大小完全相同的“●”按一定规律所组成,其中图①共有6个黑点,图②共有9个黑点,图③共有12个黑点…,按此规律排列,则图⑦中黑点的个数为( ) A、21 B、24 C、27 D、30
A、21 B、24 C、27 D、30二、填空题(共4小题,满分16分,每小题4分)
-
13. 要想了解九年级1500名学生的心理健康评估报告,从中抽取了300名学生的心理健康评估报告进行统计分析,以下说法:①1500名学生是总体;②每名学生的心理健康评估报告是个体;③被抽取的300名学生是总体的一个样本;④300是样本容量.其中正确的是 .14. 在校秋季运动会中,跳远比赛的及格线为4m . 小明跳出了4.25m , 记作+0.25m , 那么小刚跳出了3.84m , 记作 m .15. 如果单项式﹣xyb+1与2xa+2y3是同类项,则ax+b=0的解为 .16. 如图,O为直线DA上一点,∠AOB=120°,OE为∠AOB的平分线,∠COB=90°,则∠EOC的度数是 .

三、解答题(共8小题,满分86分)
-
17. 现定义一种新运算“*”,对任意有理数a、b , 规定 a*b=ab+a﹣b , 例如:1*2=1×2+1﹣2.(1)、求 2*(﹣3)的值;(2)、求(﹣3)*[(﹣2)*5]的值.18. 若一个两位数十位、个位上的数字分别为m、n , 我们可将这个两位数记为 , 即: .(1)、若 , 求x的值;(2)、若 , 求的值.19. 如图是由棱长都为2cm的小正方体组成的简单几何体.
 (1)、请在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、求出该几何体的体积和表面积.20. 苏州市某初中学校对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
(1)、请在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、求出该几何体的体积和表面积.20. 苏州市某初中学校对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.时间(小时)
频数(人数)
频率
0≤t<0.5
4
0.1
0.5≤t<1
a
0.3
1≤t<1.5
10
0.25
1.5≤t<2
8
b
2≤t<2.5
6
0.15
合计
1
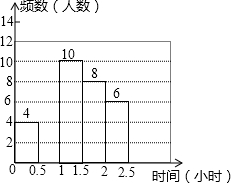 (1)、a= , b=;(2)、补全频数分布直方图;(3)、请估计该校1500名初中学生中,约有多少学生在1.5小时以内完成家庭作业.21. 已知A=3x2+ax﹣3y+2,B=bx2x﹣2y+4,且A与B的3倍的差的值与x的取值无关,求代数式﹣ab[a(4b﹣a+6)]﹣3(2ab2a2bab)的值.22. 对于任何数,规定一种新运算ad﹣bc , 例如:1×4﹣2×3=﹣2.(1)、按照这个规定,请你计算的值;(2)、按照这个规定,请你计算当x、y满足|x﹣2|+(y+3)2=0时,求的值.23. 甲、乙两人分别从相距2.5km的两地沿同一条公路同时同向出发进行骑自行车训练.已知甲、乙两人的速度分别为12.5km/h , 15km/h , 经过几小时两人相距3km?
(1)、a= , b=;(2)、补全频数分布直方图;(3)、请估计该校1500名初中学生中,约有多少学生在1.5小时以内完成家庭作业.21. 已知A=3x2+ax﹣3y+2,B=bx2x﹣2y+4,且A与B的3倍的差的值与x的取值无关,求代数式﹣ab[a(4b﹣a+6)]﹣3(2ab2a2bab)的值.22. 对于任何数,规定一种新运算ad﹣bc , 例如:1×4﹣2×3=﹣2.(1)、按照这个规定,请你计算的值;(2)、按照这个规定,请你计算当x、y满足|x﹣2|+(y+3)2=0时,求的值.23. 甲、乙两人分别从相距2.5km的两地沿同一条公路同时同向出发进行骑自行车训练.已知甲、乙两人的速度分别为12.5km/h , 15km/h , 经过几小时两人相距3km?解:设经过xh两人相距3km ,
根据题意,得15x﹣(12.5x+2.5)=3,
解得x=2.2.
答:经过2.2h两人相距3km .
以上解答过程正确吗?若不正确,请指出错误,并给出正确的解答过程.
24. 已知,C , D为线段AB上两点,C在D的左边,AB=a , CD=b , 且a , b满足(a﹣120)2+|4b﹣a|=0. (1)、a= , b=;(2)、如图1,若M是线段AD的中点,N是线段BC的中点,求线段MN的长;(3)、线段CD在线段AB上从端点D与点B重合的位置出发,以3cm/s的速度沿射线BA的方向运动,同时点P以相同速度从点A出发沿射线AB的方向运动,当点P与点D相遇时,点P原路返回且速度加倍,线段CD的运动状态不变,直到点C到达点A时线段CD和点P同时停止运动,设运动时间为t s , 在此运动过程中,当t为多少s时线段PC=10cm?
(1)、a= , b=;(2)、如图1,若M是线段AD的中点,N是线段BC的中点,求线段MN的长;(3)、线段CD在线段AB上从端点D与点B重合的位置出发,以3cm/s的速度沿射线BA的方向运动,同时点P以相同速度从点A出发沿射线AB的方向运动,当点P与点D相遇时,点P原路返回且速度加倍,线段CD的运动状态不变,直到点C到达点A时线段CD和点P同时停止运动,设运动时间为t s , 在此运动过程中,当t为多少s时线段PC=10cm?