浙江省温州市瑞安市2023-2024学年五年级上学期数学期末试卷
试卷更新日期:2024-02-01 类型:期末考试
一、我会选(下面的选项中只有一个正确答案,每题2分,共20分)
-
1. 下列各式中,得数与10.1×4.8相等的算式是( )A、1.01×48 B、101×0.048 C、1010×0.48 D、0.101×482. 果农们要将68.4kg的陶山甘蔗装进纸箱,每个纸箱最多可以装4.5kg陶山甘蔗。装这些陶山甘蔗至少需要准备( )个纸箱。A、15 B、15.2 C、16 D、173. 17世纪中叶,浪漫的数学家笛卡尔在研究中推导出一个方程r=a(1﹣sinθ),后来的研究人员利用这个方程画出了一个封闭的图形,形状就像爱心,也称“爱心公式”。把这个图案画在方格纸上,如图(图中每个小方格的面积是1cm2)。这个心形图案的面积约为( )cm2。
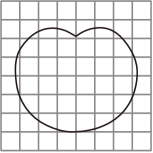 A、20 B、30 C、42 D、484. 一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。A、红球 B、白球 C、黑球 D、黄球5. 与方程5y=15的解相同的方程是( )A、3y﹣4=8 B、3y=1.8 C、2y+5=11 D、18÷y=36. 妈妈去瑞安市农贸市场批发了一些阿克苏苹果,但不小心把收据弄脏了。那么,这些苹果的总价可能是( )
A、20 B、30 C、42 D、484. 一个盒子里有6颗红球、8颗白球、15颗黑球和4颗黄球,且大小相同,从盒中摸一个球,摸出( )的可能性最大。A、红球 B、白球 C、黑球 D、黄球5. 与方程5y=15的解相同的方程是( )A、3y﹣4=8 B、3y=1.8 C、2y+5=11 D、18÷y=36. 妈妈去瑞安市农贸市场批发了一些阿克苏苹果,但不小心把收据弄脏了。那么,这些苹果的总价可能是( ) A、54.19元 B、58.24元 C、72.09元 D、80.12元7. 下列选项中不能用方程“2x+8=14”来表示的是( )A、
A、54.19元 B、58.24元 C、72.09元 D、80.12元7. 下列选项中不能用方程“2x+8=14”来表示的是( )A、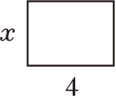 长方形的周长是14
B、
长方形的周长是14
B、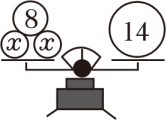 C、某小组男生有x人,女生比男生多8人,该小组一共有14人
D、
C、某小组男生有x人,女生比男生多8人,该小组一共有14人
D、 8. 明明在解决“王阿姨用一根12.4m长的丝带包装礼盒,每包装一个礼盒要用1.5m丝带。这根丝带最多可以包装多少个礼盒?”时,列出了竖式(如图)。那么,竖式中的余数“4”表示( )
8. 明明在解决“王阿姨用一根12.4m长的丝带包装礼盒,每包装一个礼盒要用1.5m丝带。这根丝带最多可以包装多少个礼盒?”时,列出了竖式(如图)。那么,竖式中的余数“4”表示( ) A、0.4m B、4m C、0.4个礼盒 D、4个礼盒9. a、b、c对应的点都是一位小数,在数轴上表示如图。下面( )的计算结果与c点对应的数最接近。
A、0.4m B、4m C、0.4个礼盒 D、4个礼盒9. a、b、c对应的点都是一位小数,在数轴上表示如图。下面( )的计算结果与c点对应的数最接近。 A、b﹣a B、a×b C、a÷b D、b÷a10. 如图是由边长为8cm和6cm的两个正方形组合而成,点P从C点出发,以每秒1cm的速度沿着该图形的最外围线段移动,当点P运动至( )秒时,点P与点A、点B所组成的三角形ABP面积最大。
A、b﹣a B、a×b C、a÷b D、b÷a10. 如图是由边长为8cm和6cm的两个正方形组合而成,点P从C点出发,以每秒1cm的速度沿着该图形的最外围线段移动,当点P运动至( )秒时,点P与点A、点B所组成的三角形ABP面积最大。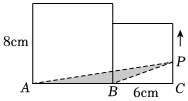 A、5 B、10 C、15 D、25
A、5 B、10 C、15 D、25二、我会填(每题2分,共20分)
-
11. 2.08×6.2的积是 位小数。1.6÷1.2的商用循环小数表示是 。12. “宸宸”是2023年杭州亚运会的吉祥物之一。制作一个这样的吉祥物需要0.8米布,15米的布最多能做 个这样的吉祥物;如果每个吉祥物售价20.5元,一共可以卖 元。13. 在下面的横线上填上“>”“<”或“=”。
12.22×0.98 12.22 0.64÷0.8 64÷8
1.6+0.4 1.6×0.4 4.5÷0.5 4.5×2
14. 一个两位小数“四舍五入”后得到的近似数是5.4,这个两位小数最大是 , 最小是 。15. 某新能源电动车行驶400千米耗电80千瓦时。那么这种新能源电动车耗电1千瓦时,能行驶 千米;如果行驶1千米,耗电 千瓦时。16. 如图,为了防止衣架滑动,爸爸在一根晾衣竿上等距离打了20个圆孔。那么,这些圆孔将晾衣竿平均分成了 小段,这根晾衣竿的长是 m。 17. 根据等式性质,如果5x=1012y , 那么,10x=;5x+1=。18. 如图直线l是两个三角形的对称轴,已知C点用数对(8,2)表示,那么,A点用数对表示为 , B点用数对表示为 。
17. 根据等式性质,如果5x=1012y , 那么,10x=;5x+1=。18. 如图直线l是两个三角形的对称轴,已知C点用数对(8,2)表示,那么,A点用数对表示为 , B点用数对表示为 。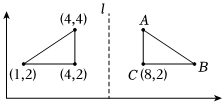 19. 我国古代数学家刘徽利用“出入相补”原理计算梯形面积。如图,转化后的平行四边形的底是10cm , 高是hcm , 原梯形的高是 cm , 面积是 cm2。
19. 我国古代数学家刘徽利用“出入相补”原理计算梯形面积。如图,转化后的平行四边形的底是10cm , 高是hcm , 原梯形的高是 cm , 面积是 cm2。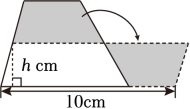 20. 如图,根据正方形的个数及顶点个数的规律,请将表格补充完整。
20. 如图,根据正方形的个数及顶点个数的规律,请将表格补充完整。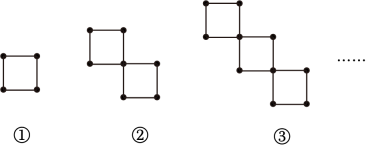
正方形的个数
1
2
3
4
……
n
顶点个数
4
7
10
……
三、我会算(4+5+6+12=27分)
-
21. 直接写得数。
1.43+6.07=
11.7﹣8.9=
3.2÷0.8=
0.58+0.42×0=
4.5÷5=
1.25×0.8=
0.5×0.6=
1.8×4÷1.8×4=
22. 列竖式计算,带★的要验算。★1.06×0.9 3.82÷2.7(保留一位小数)
23. 解方程。2x+3.5=10.7 5x﹣x=9.6 24. 递等式计算,能简算的要简算。12.5×20.24×8 8.8÷(3.2+0.3×4)
0.63×38+62×0.63 5.4÷0.4÷2.5
四、我会操作(每题2分,共6分)
-
25. 观察如图方格图,按要求完成题目。(每个小方格边长为1cm)
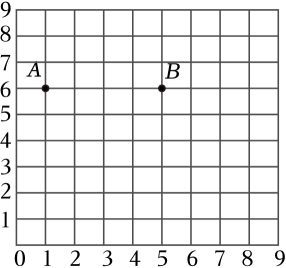 (1)、A点用数对表示为(1,6),B点用数对表示为( , )请在图中标出点C(4,3)的位置。(2)、依次连接A、B、C三点组成三角形,这个三角形的面积是 cm2。(3)、请在方格图上画一个与三角形ABC面积相等的三角形。
(1)、A点用数对表示为(1,6),B点用数对表示为( , )请在图中标出点C(4,3)的位置。(2)、依次连接A、B、C三点组成三角形,这个三角形的面积是 cm2。(3)、请在方格图上画一个与三角形ABC面积相等的三角形。五、我会解决问题(第28、29、30题5分,其它每题4分,共27分)
-
26. 瑞安某公司食堂1月份新购进176千克花生油,平均每天用5.5千克,这些油够这个月用吗?27. 科学纪录片《地球脉动》一集60分钟,李华看了20分钟后,把播放速度调整至1.25倍。照这个速度,剩余部分还需多少分钟看完?
 28. 杭州第19届亚运会,中国体育代表团获得201枚金牌,比日本体育代表团获得金牌数的4倍少7枚。日本体育代表团获金牌数多少枚?(先写出等量关系式,再列方程解答)
28. 杭州第19届亚运会,中国体育代表团获得201枚金牌,比日本体育代表团获得金牌数的4倍少7枚。日本体育代表团获金牌数多少枚?(先写出等量关系式,再列方程解答)等量关系式:( )
列方程解决:( )
29. 如图是某种植果园基地的示意图。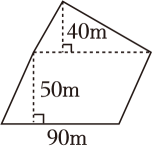 (1)、求这个果园的面积是多少m2?(2)、如果每棵果树占地10m2 , 这个果园共有多少棵果树?30. 小丽使用微信支付(如图)在文具店里买了一些笔和笔记本。买3支笔花了6.9元,剩余的钱买了4本笔记本,每本笔记本多少元?
(1)、求这个果园的面积是多少m2?(2)、如果每棵果树占地10m2 , 这个果园共有多少棵果树?30. 小丽使用微信支付(如图)在文具店里买了一些笔和笔记本。买3支笔花了6.9元,剩余的钱买了4本笔记本,每本笔记本多少元? 31. 温州轨道交通S2线于2023年9月5日开通运营,采取分段计价,如图所示。5元钱最多可以乘多少千米?
31. 温州轨道交通S2线于2023年9月5日开通运营,采取分段计价,如图所示。5元钱最多可以乘多少千米?行驶的路程/千米
计费标准
0~4(含4km)
2元
4~28(含28km)
每1元可乘4km
(不足4km的按4km计算)
28~64(含64km)
每1元可乘6km
(不足6km按6km计算)
六、我会挑战(附加题,共10分)
-
32. 阅读与解答。
同学们,这个学期我们学习了多边形面积的有关知识,让我们进一步探索和解决如下问题:
1899年,奥地利数学家皮克将多边形放到格点中研究,发现多边形面积与多边形上内部钉子数、边上钉子数之间的规律,并进行了证明。这个规律被誉为史上“最重要的100个定理”之一。
皮克把平面图形放到边长1cm的点子图上,通过数平面图形内部和边上“点”的个数来计算面积。
(1)、【初探规律】
观察如图的多边形,根据你的发现完成表格并填空。
图形(序号)
①
②
③
④
内部点数a
1个
1个
1个
1个
边上点数b
4个
5个
个
7个
图形面积S
2cm2
2.5cm2
3cm2
cm2
从表中可以发现:内部点数a都为1时,图形面积S与边上点数b之间的数量关系可以表示为:S=。
(2)、【完善规律】
观察如图的多边形,根据你的发现完成表格并填空。
图形(序号)
⑤
⑥
⑦
⑧
内部点数a
2个
3个
个
5个
边上点数b
8个
8个
8个
8个
图形面积S
5cm2
6cm2
7cm2
cm2
从这个表中进一步发现:内部点数a增多时,用上面的数量关系根据边上点数b直接得出图形面积S不成立了,需将内部点数a放入考虑寻找规律,原来的数量关系可完善为:S=。像这样计算面积的方法叫格点法,也叫皮克定理。
(3)、【应用规律】
请在如图的点子图上画一个面积是6.5cm2 , 且内部点数为5个的多边形。
-