2024年北师大版数学七年级下册单元清测试(第五章)培优卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示,在中,按下列步骤作图:
2. 如图所示,在中,按下列步骤作图:第一步:在上分别截取 , 使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
 A、 B、 C、 D、3. 如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=25°,则∠ADC的度数是( )
A、 B、 C、 D、3. 如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=25°,则∠ADC的度数是( ) A、45° B、60° C、75° D、70°4. 如图,在△ABC中,AC = 10,AB的垂直平分线交AB于点M,交AC于点D,△BDC的周长为18,则BC的长为( )
A、45° B、60° C、75° D、70°4. 如图,在△ABC中,AC = 10,AB的垂直平分线交AB于点M,交AC于点D,△BDC的周长为18,则BC的长为( ) A、4 B、6 C、8 D、105. 如图,有A、B、C三个居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
A、4 B、6 C、8 D、105. 如图,有A、B、C三个居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( ) A、的三条中线的交点处 B、三边的垂直平分线的交点处 C、三条角平分线的交点处 D、三条高所在直线的交点处6. 等腰三角形的一个角是50°,则它顶角的度数是( )A、80°或50° B、80° C、80°或65° D、65°7. 如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( )
A、的三条中线的交点处 B、三边的垂直平分线的交点处 C、三条角平分线的交点处 D、三条高所在直线的交点处6. 等腰三角形的一个角是50°,则它顶角的度数是( )A、80°或50° B、80° C、80°或65° D、65°7. 如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( ) A、AC=A′C′ B、BO=B′O C、AA′⊥MN D、AB B′C′8.
A、AC=A′C′ B、BO=B′O C、AA′⊥MN D、AB B′C′8.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
 A、48° B、36° C、30° D、24°9. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )
A、48° B、36° C、30° D、24°9. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )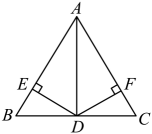 A、①④ B、②④ C、②③④ D、①②③④10. 如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( )
A、①④ B、②④ C、②③④ D、①②③④10. 如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 如图,已知 , 点D在上,以点B为圆心,长为半径画弧,交于点E,连接 , 则的度数是 度.
 12. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .
12. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .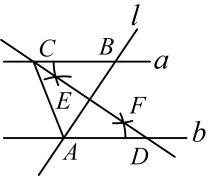 13. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。
13. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是。 14. 如图,在Rt ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为°.
14. 如图,在Rt ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为°. 15. 如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E , F分别是BC , DC上的点,当△AEF的周长最小时,∠EAF的度数为 .
15. 如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E , F分别是BC , DC上的点,当△AEF的周长最小时,∠EAF的度数为 . 16. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .
16. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .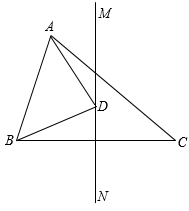
三、解答题
-
17. 如图,方格纸中每个小方格都是边长为1个单位的正方形,已知 的三个顶点在格点上.
 (1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小18. 已知:如图,AD平分∠CAB,过点D作DM⊥AB于点M,DN⊥AC的延长线于点N,且∠NCD=∠B.求证:CN=BM.
(1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小18. 已知:如图,AD平分∠CAB,过点D作DM⊥AB于点M,DN⊥AC的延长线于点N,且∠NCD=∠B.求证:CN=BM. 19. 如图,点D是线段的中点, , 点P是线段上的一点,射线交边于点E , 于点H , 过B作于点F .
19. 如图,点D是线段的中点, , 点P是线段上的一点,射线交边于点E , 于点H , 过B作于点F .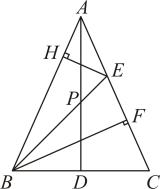 (1)、求证:;(2)、如果 , 求证: .20. 已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)、求证:;(2)、如果 , 求证: .20. 已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M. (1)、若AC=6,DM=2,求△ACD的面积;(2)、求证:AC=BM+CM.21. 如图,在△ABC中,AB=AC,P为BC的中点,D,E分别为AB,AC上的点,且∠BDP=∠CEP.
(1)、若AC=6,DM=2,求△ACD的面积;(2)、求证:AC=BM+CM.21. 如图,在△ABC中,AB=AC,P为BC的中点,D,E分别为AB,AC上的点,且∠BDP=∠CEP.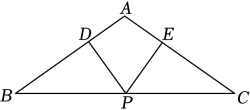 (1)、求证:△BDP≌△CEP .(2)、若PD⊥AB , ∠A=110°,求∠EPC的度数.22. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)、求证:△BDP≌△CEP .(2)、若PD⊥AB , ∠A=110°,求∠EPC的度数.22. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.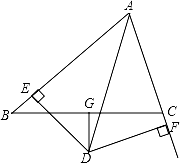 (1)、求证:BE=CF;(2)、如果AB=8,AC=6,求AE、BE的长.23. 数学模型学习与应用:
(1)、求证:BE=CF;(2)、如果AB=8,AC=6,求AE、BE的长.23. 数学模型学习与应用:白日登山望峰火,黄昏饮马傍交河.——《古从军行》唐李欣
模型学习:诗中隐含着一个有趣的数学问题,我们称之为“将军饮马”问题.关键是利用轴对称变换,把直线同侧两点的折线问题转化为直线两侧的线段问题,从而解决距离和最短的一类问题,“将军饮马”问题的数学模型如图1所示:在直线l上存在点P , 使PA+PB的值最小.
作法:作A点关于直线l的对称点A',连接A'B , A'B与直线l的交点即为点P . 此时PA+PB的值最小.
 (1)、模型应用:
(1)、模型应用:如图2,已知△ABC为等边三角形,高AH=8cm , P为AH上一动点,D为AB的中点.
①当PD+PB的最小值时,在图中确定点P的位置(要有必要的画图痕迹,不用写画法).
②则PD+PB的最小值为 ▲ cm .
(2)、模型变式:如图3所示,某地有块三角形空地AOB , 已知∠AOB=30°,P是△AOB内一点,连接PO后测得PO=10米,现当地政府欲在三角形空地AOB中修一个三角形花坛PQR , 点Q、R分别是OA , OB边上的任意一点(不与各边顶点重合),求△PQR周长的最小值.
24. 综合与实践(1)、问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得 , 连接 , 以为边作等边三角形 , 则就是的平分线.
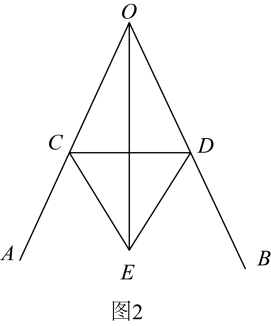
请写出平分的依据:;
(2)、类比迁移:
小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边 , 上分别取 , 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
(3)、拓展实践:
小明将研究应用于实践.如图4,校园的两条小路和 , 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)