2024年北师大版数学七年级下册单元清测试(第五章) 基础卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 等腰三角形的两边分别为12和6,则这个三角形的周长是( )A、24 B、18 C、30 D、24或303. 等腰三角形的一个内角是70°,则它顶角的度数是( )A、 B、 或 C、 或 D、4. 如图,平分 , 于点 , 点是射线上的一个动点,若 , 则的最小值为( )
2. 等腰三角形的两边分别为12和6,则这个三角形的周长是( )A、24 B、18 C、30 D、24或303. 等腰三角形的一个内角是70°,则它顶角的度数是( )A、 B、 或 C、 或 D、4. 如图,平分 , 于点 , 点是射线上的一个动点,若 , 则的最小值为( ) A、2 B、3 C、4 D、55. 如图,在中,是的垂直平分线, , , 则的周长为( )
A、2 B、3 C、4 D、55. 如图,在中,是的垂直平分线, , , 则的周长为( ) A、 B、 C、 D、6. 如图,在△ABC中,∠C=90°,BD平分∠ABC,CD=3,则D到AB的距离是( )
A、 B、 C、 D、6. 如图,在△ABC中,∠C=90°,BD平分∠ABC,CD=3,则D到AB的距离是( ) A、2 B、3 C、4 D、57. 如图,中,D点在上,将D点分别以为对称轴,画出对称点E、F,并连接 , 根据图中标示的角度,的度数为( )
A、2 B、3 C、4 D、57. 如图,中,D点在上,将D点分别以为对称轴,画出对称点E、F,并连接 , 根据图中标示的角度,的度数为( ) A、 B、 C、 D、8. 如图,直线、、表示三条相互交叉的公路,交叉口分别为、、 , 形成一个 , 现要在三条公路形成的三角区域内建一座加油站,要求到、、三个交叉口的距离相等,则加油站应建在( )
A、 B、 C、 D、8. 如图,直线、、表示三条相互交叉的公路,交叉口分别为、、 , 形成一个 , 现要在三条公路形成的三角区域内建一座加油站,要求到、、三个交叉口的距离相等,则加油站应建在( ) A、的三条高的交点处 B、的三条角平分线的交点处 C、的三条中线的交点处 D、的三条边的垂直平分线的交点处9. 如图,是线段的垂直平分线,则下列结论一定正确的是( )
A、的三条高的交点处 B、的三条角平分线的交点处 C、的三条中线的交点处 D、的三条边的垂直平分线的交点处9. 如图,是线段的垂直平分线,则下列结论一定正确的是( )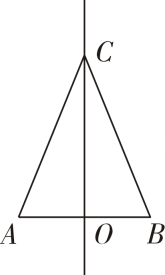 A、
A、
B、
C、
D、10. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )

 A、①③ B、①② C、②③ D、①②③
A、①③ B、①② C、②③ D、①②③二、填空题
-
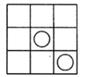
11. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。
 12. 如图,在中,是的垂直平分线.若 , , 则的周长是.
12. 如图,在中,是的垂直平分线.若 , , 则的周长是.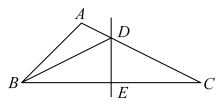 13. 如图,在中, , 按以下步骤作图:①以点为圆心,以小于长为半径作弧,分别交于点 , ;②分别以 , 为圆心,以大于的长为半径作弧,在内两弧交于点;③作射线 , 交于点 . 若点到的距离为 , 则的长为 .
13. 如图,在中, , 按以下步骤作图:①以点为圆心,以小于长为半径作弧,分别交于点 , ;②分别以 , 为圆心,以大于的长为半径作弧,在内两弧交于点;③作射线 , 交于点 . 若点到的距离为 , 则的长为 .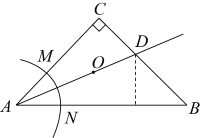 14. 如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=度.
14. 如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=度.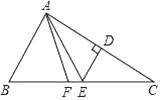 15. 如图,与△关于直线对称,则的度数为 .
15. 如图,与△关于直线对称,则的度数为 . 16. 如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC,DE⊥AB于点E,AC=9,AD=5,则DE的长为 .
16. 如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC,DE⊥AB于点E,AC=9,AD=5,则DE的长为 .
三、解答题
-
17. 如图是4×4正方形网格,其中已有3个小方格涂成了阴影.现在要从其余13个白色小方格中选出一个也涂成阴影,使整个涂成阴影的图形成为轴对称图形,请在图中补全图形,并画出它们各自的对称轴.(要求画出3种不同方法)
 18. 如图,网格中的和是轴对称图形.
18. 如图,网格中的和是轴对称图形.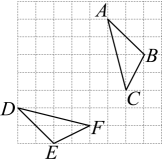 (1)、利用网格线,作出和的对称轴;(2)、如果每个小正方形的边长为1,则的面积为 .19. 如图,在中, , 为边上的中线.以点为圆心,的长为半径画弧,与 , 分别交于点 , , 连接 , .
(1)、利用网格线,作出和的对称轴;(2)、如果每个小正方形的边长为1,则的面积为 .19. 如图,在中, , 为边上的中线.以点为圆心,的长为半径画弧,与 , 分别交于点 , , 连接 , . (1)、求证:;(2)、若 , 求的度数.20. 如图,中, , 的垂直平分线分别交、于点、 .
(1)、求证:;(2)、若 , 求的度数.20. 如图,中, , 的垂直平分线分别交、于点、 . (1)、若 , 求的度数;(2)、若 , 的长为5,求的周长.21. 如图,在四边形ABCD中,AD∥BC,∠DAB的平分线交BC的延长线于点E,BG⊥AE,垂足为点F,交CD于点G.
(1)、若 , 求的度数;(2)、若 , 的长为5,求的周长.21. 如图,在四边形ABCD中,AD∥BC,∠DAB的平分线交BC的延长线于点E,BG⊥AE,垂足为点F,交CD于点G. (1)、求证:BG平分∠ABE;(2)、若∠DCB=100°,∠DAB=60°,求∠BGC的度数.22. 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)、求证:BG平分∠ABE;(2)、若∠DCB=100°,∠DAB=60°,求∠BGC的度数.22. 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD. (1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.23. 如图,在中,的垂直平分线交于点 , 边的垂直平分线交于点E.
(1)、求证:△BCE≌△DCF;(2)、求证:AB+AD=2AE.23. 如图,在中,的垂直平分线交于点 , 边的垂直平分线交于点E. (1)、已知的周长 , 求的长;(2)、若 , , 求的度数.24.(1)、[感知]
(1)、已知的周长 , 求的长;(2)、若 , , 求的度数.24.(1)、[感知]
如图①,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F , 且BD=CF . 若DE⊥BC , 则∠DFC的大小是度;
(2)、[探究]如图②,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F , 且BD=CF . 求证:BE=CD;
(3)、[应用]在图③中,若D是边BC的中点,且AB=2,其它条件不变,如图③所示,则四边形AEDF的周长为 .