2024年北师大版数学七年级下册周测卷(第五章 第3(第2课时 )-4节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G,连结DG,EG.添加下列条件,不能使BG=CG成立的是( )
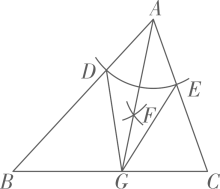 A、 B、 C、 D、2. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、
A、 B、 C、 D、2. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、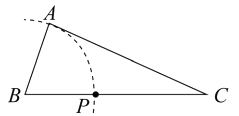 B、
B、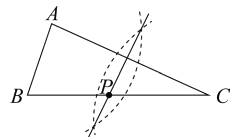 C、
C、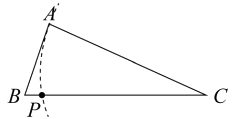 D、
D、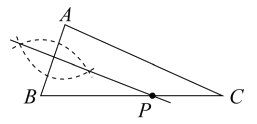 3. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
3. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )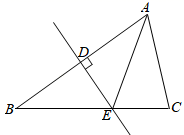 A、2 B、4 C、6 D、84. 如图,直线 , 直线l分别交 , 于点M,N,的平分线交于点F, , 则( )
A、2 B、4 C、6 D、84. 如图,直线 , 直线l分别交 , 于点M,N,的平分线交于点F, , 则( ) A、 B、 C、 D、5. 如图, , 平分 , 则( )
A、 B、 C、 D、5. 如图, , 平分 , 则( ) A、 B、 C、 D、6. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( )
A、 B、 C、 D、6. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( ) A、 B、 C、 D、7. 如图,在 中, , ,点D,P分别是图中所作直线和射线与 , 的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )
A、 B、 C、 D、7. 如图,在 中, , ,点D,P分别是图中所作直线和射线与 , 的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )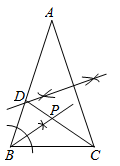 A、 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )
A、 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )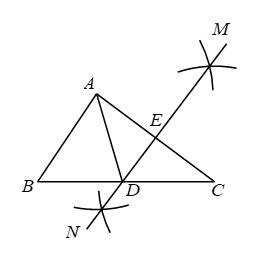 A、13 B、14 C、15 D、169. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.
A、13 B、14 C、15 D、169. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.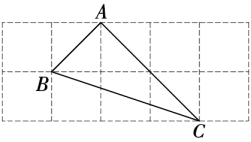 A、1 B、2 C、3 D、410. 如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A、1 B、2 C、3 D、410. 如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.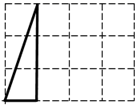 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
11. 在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有种.
 12.
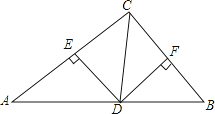
12.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
 13. 如图,直线 , 直线分别与 , 交于点 , , 小明同学利用尺规按以下步骤作图:
13. 如图,直线 , 直线分别与 , 交于点 , , 小明同学利用尺规按以下步骤作图:
⑴点为圆心,以任意长为半径作弧交射线于点 , 交射线于点;
⑵分别以点 , 为圆心,以大于的长为半径作弧,两弧在内交于点;
⑶作射线交直线于点;若 , 则度.
14. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.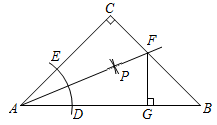 15. 如图,在 中, ,分别以点A , B为圆心,以大于 长为半径画弧,两弧交于点D , E . 作直线DE , 交BC于点M . 分别以点A , C为圆心,以大于 长为半径画弧,两弧交于点F , G . 作直线FG , 交BC于点N . 连接AM , AN . 若 ,则 .
15. 如图,在 中, ,分别以点A , B为圆心,以大于 长为半径画弧,两弧交于点D , E . 作直线DE , 交BC于点M . 分别以点A , C为圆心,以大于 长为半径画弧,两弧交于点F , G . 作直线FG , 交BC于点N . 连接AM , AN . 若 ,则 .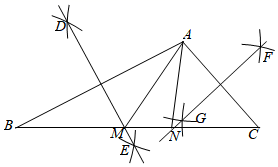 16. 如图,等腰中, , , 边的垂直平分线交于点 , 连接 , 则的度数是 .
16. 如图,等腰中, , , 边的垂直平分线交于点 , 连接 , 则的度数是 .
三、解答题
-
17. 如图,在所给网格图(每小格均为边长是1的正方形,每个小正方形的顶点称为格点)中完成下列各题:
 (1)、画出格点(顶点均在格点上)关于直线对称的图形;(2)、在上画出点P , 使最小;(3)、在上画出点Q , 使Q到B , C两点的距离相等;(4)、四边形的面积为 .18. 如图所示,在中,为的中点, , 交的平分线于点 , 于点 , 交延长线于点 . 求证: .
(1)、画出格点(顶点均在格点上)关于直线对称的图形;(2)、在上画出点P , 使最小;(3)、在上画出点Q , 使Q到B , C两点的距离相等;(4)、四边形的面积为 .18. 如图所示,在中,为的中点, , 交的平分线于点 , 于点 , 交延长线于点 . 求证: . 19. 如图,已知中,是的角平分线,于E点.
19. 如图,已知中,是的角平分线,于E点.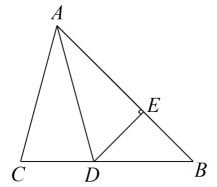 (1)、求的度数;(2)、若 , 求 .20. 如图,BD是∠ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)、求的度数;(2)、若 , 求 .20. 如图,BD是∠ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F. (1)、试说明:BE=BF;(2)、若△ABC的面积为81,AB=15,DE=6,则BC的长为21. 如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.
(1)、试说明:BE=BF;(2)、若△ABC的面积为81,AB=15,DE=6,则BC的长为21. 如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF. (1)、CF=EB;(2)、∠CBA+∠AFD=180°.22. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , .
(1)、CF=EB;(2)、∠CBA+∠AFD=180°.22. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , . (1)、【发现问题】
(1)、【发现问题】如图①,当 , 时,则与的数量关系是 .
(2)、【探究问题】如图②,点C , D在射线 , 上滑动,且 , 当时,与在【发现问题】中的数量关系还成立吗?说明理由.
23. 请完成下面的说明: (1)、如图①所示,△ABC的外角平分线交于点G , 试说明∠BGC=90°﹣∠A .(2)、如图②所示,若△ABC的内角平分线交于点I , 试说明∠BIC=90°+∠A .(3)、根据(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?24. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”.
(1)、如图①所示,△ABC的外角平分线交于点G , 试说明∠BGC=90°﹣∠A .(2)、如图②所示,若△ABC的内角平分线交于点I , 试说明∠BIC=90°+∠A .(3)、根据(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?24. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”. (1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)
(1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)①垂线段最短:②垂直平分线的性质;③角平分线的性质;④三角形内角和定理
(2)、猜想论证:如图2,当为任意角时,猜想DA与DC的数量关系,并给予证明;(3)、探究应用:如图3,在等腰中, , BD平分 ,求证:.