2024年北师大版数学七年级下册周测卷(第五章 第3(第2课时 )-4节)基础卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
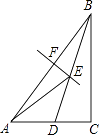
1. 如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( )
 A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD2. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、
A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD2. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、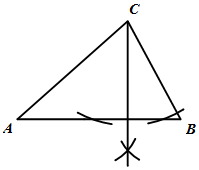 B、
B、 C、
C、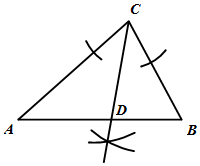 D、
D、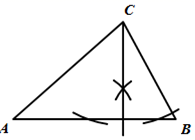 3. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
3. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )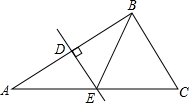 A、12 B、13 C、14 D、154. 如图,点P是∠AOB平分线上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA 的距离是( )
A、12 B、13 C、14 D、154. 如图,点P是∠AOB平分线上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA 的距离是( )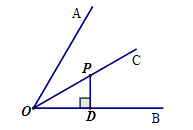 A、1 B、2 C、 D、45.
A、1 B、2 C、 D、45.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线。则对应作法错误的是( )
 A、 ① B、② C、③ D、④6. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、 ① B、② C、③ D、④6. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )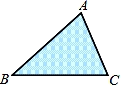 A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点7. 如图,在中,是和角平分线的交点,则的度数为( ).
A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点7. 如图,在中,是和角平分线的交点,则的度数为( ).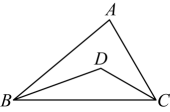 A、 B、 C、 D、8. 用尺规作图作一个已知角的平分线的示意图如图如示,以O为圆心,以适当长度为半径作弧,分别交、于M、N点,再分别以M、N点为圆心,以大于的长度为半径作弧,两弧交于C点,连接 , 则能说明的依据是( )
A、 B、 C、 D、8. 用尺规作图作一个已知角的平分线的示意图如图如示,以O为圆心,以适当长度为半径作弧,分别交、于M、N点,再分别以M、N点为圆心,以大于的长度为半径作弧,两弧交于C点,连接 , 则能说明的依据是( ) A、 B、 C、 D、角平分线上的点到角两边的距离相等9. 如图,线段AB,AC的垂直平分线相交于点P,则PB与PC的数量关系是( )
A、 B、 C、 D、角平分线上的点到角两边的距离相等9. 如图,线段AB,AC的垂直平分线相交于点P,则PB与PC的数量关系是( ) A、PB>PC B、PB=PC C、PB<PC D、PB=2PC10. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
A、PB>PC B、PB=PC C、PB<PC D、PB=2PC10. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
11. 如图,在 的正方形网格中,选取13个格点,以其中的三个格点A,B,C为顶点画 ,请你在图中以选取的格点为顶点再画出一个 ,使 与 成轴对称.这样的P点有个.(填P点的个数)
 12. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
12. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种. 13. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.
13. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.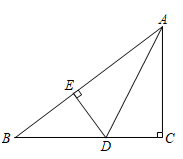 14. 如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=6,则△BCE的面积为 .
14. 如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=6,则△BCE的面积为 .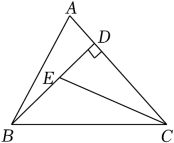 15. 如图,在△ABC中,边AB的垂直平分线分别交BC于点D,交AB于点E.若AE=3,△ADC的周长为8,则△ABC的周长为 .
15. 如图,在△ABC中,边AB的垂直平分线分别交BC于点D,交AB于点E.若AE=3,△ADC的周长为8,则△ABC的周长为 .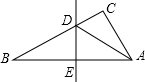 16. 如图所示,BD为∠ABC的角平分线,∠C=90°,CD=3,则点D到AB的距离是 .
16. 如图所示,BD为∠ABC的角平分线,∠C=90°,CD=3,则点D到AB的距离是 .
三、解答题
-
17. 如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,下面四个图中的三角形为格点三角形,在图中分别画出与已知三角形成轴对称(对称轴不相同)的格点三角形.
 18. 请用几何图形“△”、“‖”、“
18. 请用几何图形“△”、“‖”、“ ”(一个三角形,两条平行线,一个半圆)作为构件,尽可能构思独特且有意义的图形,并写上一两句贴切,诙谐的解说词.(至少两幅图)
”(一个三角形,两条平行线,一个半圆)作为构件,尽可能构思独特且有意义的图形,并写上一两句贴切,诙谐的解说词.(至少两幅图) 如:
 19. 如图,在正方形网格上有一个 .
19. 如图,在正方形网格上有一个 . (1)、画出关于直线的对称图形(不写画法);
(1)、画出关于直线的对称图形(不写画法);
(2)、若网格上的每个小正方形的边长为1,求的面积.20. 如图,在△ABC中,∠A=30°,∠B=60°,CE平分∠ACB.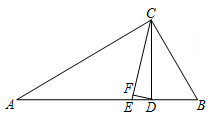 (1)、直接写出∠ACE的度数.(2)、若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.21. 已知在中, , 线段的垂直平分线交于点 , 交射线于点 , 连接 .
(1)、直接写出∠ACE的度数.(2)、若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.21. 已知在中, , 线段的垂直平分线交于点 , 交射线于点 , 连接 .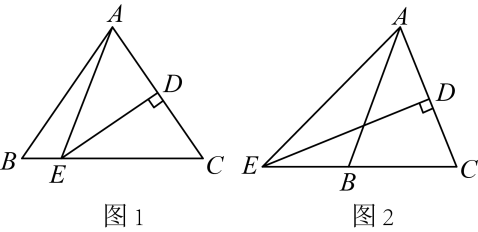 (1)、如图1,当点在边上时,若 , 求的度数;(2)、如图2,当点在延长线上时,设 , 用含的式子表示的度数22. 如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)、如图1,当点在边上时,若 , 求的度数;(2)、如图2,当点在延长线上时,设 , 用含的式子表示的度数22. 如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1) 若BC = 10 cm,试求△AMN的周长.
(2) 在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.