2024年北师大版数学七年级下册周测卷(第五章 第1-3(第1课时)节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )A、
 B、
B、 C、
C、 D、
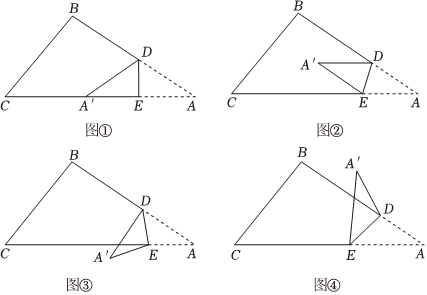
D、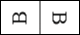 2. 如图1所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
2. 如图1所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形4. 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
3. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形4. 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )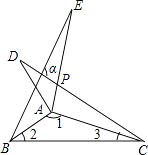 A、90° B、108° C、110° D、126°5. 如图,与关于直线对称,连接交对称轴于点 , 若 , , 则下列说法不正确的是( )
A、90° B、108° C、110° D、126°5. 如图,与关于直线对称,连接交对称轴于点 , 若 , , 则下列说法不正确的是( ) A、三角形与三角形的周长相等 B、且 C、 D、连接 , 则三条线段不仅平行而且相等6. 如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A、三角形与三角形的周长相等 B、且 C、 D、连接 , 则三条线段不仅平行而且相等6. 如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )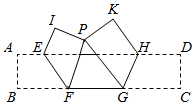 A、54° B、55° C、56° D、57°7. 如图,AB=AD , 点B关于AC的对称点E恰好落在CD上.若∠BAD=a(0°<a<180°),则∠ACB的度数为( )
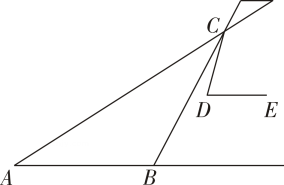
A、54° B、55° C、56° D、57°7. 如图,AB=AD , 点B关于AC的对称点E恰好落在CD上.若∠BAD=a(0°<a<180°),则∠ACB的度数为( )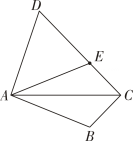 A、45° B、a﹣45° C、a D、90°﹣a8. 已知一个等腰三角形的两边长分别是4,5,则它的周长是( )A、13 B、14 C、13或14 D、9或129. 在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )
A、45° B、a﹣45° C、a D、90°﹣a8. 已知一个等腰三角形的两边长分别是4,5,则它的周长是( )A、13 B、14 C、13或14 D、9或129. 在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )
 A、16° B、28° C、44° D、45°10. 如图,≌ , 点在线段上, , 则的大小为( )
A、16° B、28° C、44° D、45°10. 如图,≌ , 点在线段上, , 则的大小为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中,若 , , , 则 .
 12. 已知,在中, , , P为直线上一点,且 , 则的度数为 .13. 如图1是长方形纸带, , 将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是.
12. 已知,在中, , , P为直线上一点,且 , 则的度数为 .13. 如图1是长方形纸带, , 将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是. 14. 如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为.
14. 如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为. 15. 如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=°.
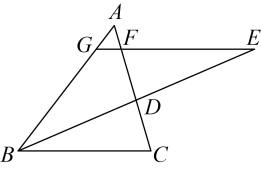
15. 如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=°. 16. 如图,中,点在上,将点分别以、为对称轴,画出对称点、.并连接、.根据图中标示的角度,则的度数为.
16. 如图,中,点在上,将点分别以、为对称轴,画出对称点、.并连接、.根据图中标示的角度,则的度数为.
三、解答题
-
17.
如图所示的方格纸中,请你把任意五个方格涂黑,使这五个方格构成一个轴对称图形(图形不能重复,至少设计三个).
 18. 如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
18. 如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上. (1)、图中点C的对应点是点 , ∠B的对应角是 ;(2)、若DE=5,BF=2,则CF的长为 ;(3)、若∠BAC=108°,∠BAE=30°,求∠EAF的度数.19. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为点E , AE与CD交于点F .
(1)、图中点C的对应点是点 , ∠B的对应角是 ;(2)、若DE=5,BF=2,则CF的长为 ;(3)、若∠BAC=108°,∠BAE=30°,求∠EAF的度数.19. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为点E , AE与CD交于点F . (1)、求证:;(2)、若 , 求的度数.20. 如图,在中,于点于点 , 交AC于点.
(1)、求证:;(2)、若 , 求的度数.20. 如图,在中,于点于点 , 交AC于点. (1)、若 , 求的度数.(2)、若是AC的中点,求证:.21. 如图,E,F分别是等边△ABC边AB,AC上的点,且AE=CF,CE,BF交于点P.
(1)、若 , 求的度数.(2)、若是AC的中点,求证:.21. 如图,E,F分别是等边△ABC边AB,AC上的点,且AE=CF,CE,BF交于点P.
 (1)、证明:CE=BF;(2)、求∠BPC的度数.22. 如图,和均为等边三角形,且点 , 在同一直线上,连结 , 交和分别于点 , 连结 .
(1)、证明:CE=BF;(2)、求∠BPC的度数.22. 如图,和均为等边三角形,且点 , 在同一直线上,连结 , 交和分别于点 , 连结 . (1)、请说出的理由;(2)、试说出的理由;(3)、试猜想是什么特殊的三角形,并加以证明.
(1)、请说出的理由;(2)、试说出的理由;(3)、试猜想是什么特殊的三角形,并加以证明.