2024年北师大版数学七年级下册周测卷(第五章 第1-3(第1课时 )节)基础卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 剪纸是中国优秀的传统文化.下列剪纸图案中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 全民阅读有助于提升一个国家、一个民族的精神力量.图书馆是开展全民阅读的重要场所.以下是我省四个地市的图书馆标志,其文字上方的图案是轴对称图形的是( )A、
2. 全民阅读有助于提升一个国家、一个民族的精神力量.图书馆是开展全民阅读的重要场所.以下是我省四个地市的图书馆标志,其文字上方的图案是轴对称图形的是( )A、 B、
B、 C、
C、 D、
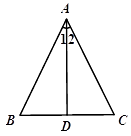
D、 3. 如图,将一个三角形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,折痕为 ,则下列结论一定正确的是( )
3. 如图,将一个三角形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,折痕为 ,则下列结论一定正确的是( )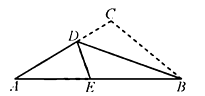 A、 B、 C、 D、4. 如图,直线 , 直线与直线a,b分别相交于点A,B,点在直线上,且 , 若 , 则的度数为( )
A、 B、 C、 D、4. 如图,直线 , 直线与直线a,b分别相交于点A,B,点在直线上,且 , 若 , 则的度数为( ) A、 B、 C、 D、5. 若等腰三角形中有两边长分别为3和7,则这个三角的周长为( )A、13 B、17 C、10 或 13 D、13 或 176. 如图,在 中 ,点 和 分别在 和 上,且 .连接 ,过点 的直线 与 平行,若 ,则 的度数为( )
A、 B、 C、 D、5. 若等腰三角形中有两边长分别为3和7,则这个三角的周长为( )A、13 B、17 C、10 或 13 D、13 或 176. 如图,在 中 ,点 和 分别在 和 上,且 .连接 ,过点 的直线 与 平行,若 ,则 的度数为( ) A、 B、 C、 D、7. 如图,若△ABC与△A′B′C′关于直线l对称,则下列结论不一定正确的是( )
A、 B、 C、 D、7. 如图,若△ABC与△A′B′C′关于直线l对称,则下列结论不一定正确的是( )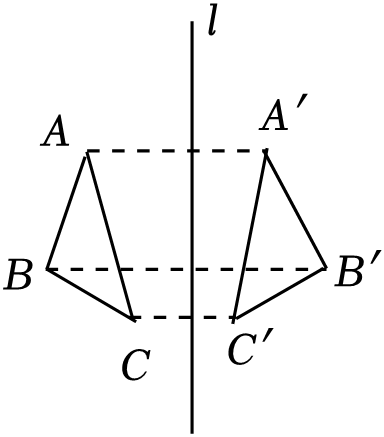 A、∠BAC=∠B′A′C′ B、△ABC≌△A′B′C′ C、直线l垂直平分 AA′ D、BB′=2AA′8. 如图,在正方形网格中有M,N两点,在直线l上求一点P,使PM+PN最短, 则点P应选在( )
A、∠BAC=∠B′A′C′ B、△ABC≌△A′B′C′ C、直线l垂直平分 AA′ D、BB′=2AA′8. 如图,在正方形网格中有M,N两点,在直线l上求一点P,使PM+PN最短, 则点P应选在( ) A、A点 B、B点 C、C点 D、D点9. 如图,和关于AD所在的直线成轴对称,E,F是中线AD上的两点,的面积是24,则图中阴影部分的面积是( )
A、A点 B、B点 C、C点 D、D点9. 如图,和关于AD所在的直线成轴对称,E,F是中线AD上的两点,的面积是24,则图中阴影部分的面积是( ) A、6 B、12 C、24 D、3010. 有一个内角是36°的等腰三角形,其它两个内角的度数分别是( )A、36°,36° B、36°,72° C、36°,108°或72°,72° D、36°,144°
A、6 B、12 C、24 D、3010. 有一个内角是36°的等腰三角形,其它两个内角的度数分别是( )A、36°,36° B、36°,72° C、36°,108°或72°,72° D、36°,144°二、填空题
-
11. 若等腰三角形的周长是 , 一腰长为 , 则这个三角形的底边长是 .12. 如图,已知AB=AC,∠1=∠2,BD=5cm,则BC=cm.
 13. 如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则∠C=度.
13. 如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则∠C=度. 14. 如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为.
14. 如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为.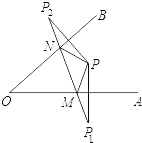 15. 如图,中,D是上一点, , , 与关于对称,则的度数为 .
15. 如图,中,D是上一点, , , 与关于对称,则的度数为 . 16. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。
16. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。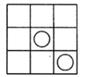
三、解答题
-
17. 在 的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形成轴对称图形,请画出三种情形.
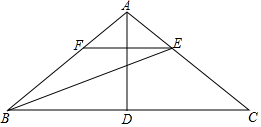
 18. 如图①,将△ABC纸片沿DE折叠,使点A落F的位置,DF与BC交于点G,EF与BC交于点M,∠A=80°,求∠1+∠2的度数;
18. 如图①,将△ABC纸片沿DE折叠,使点A落F的位置,DF与BC交于点G,EF与BC交于点M,∠A=80°,求∠1+∠2的度数; 19. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
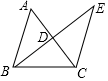
19. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长. 20. 如图,已知在△ABC中,AB=AC,CE⊥AB于点E,BD⊥AC于点D.
20. 如图,已知在△ABC中,AB=AC,CE⊥AB于点E,BD⊥AC于点D.
求证:
(1)、△ACE≌△ABD.(2)、BE=CD.21. 同学们在做题时,经常用到“在直角三角形中,角所对的直角边等于斜边的一半”这个定理,下面是两种添加辅助线的证明方法,请你选择一种进行证明.已知:在中, ,
求证:.
方法一:如图1,在AB上取一点 , 使得 , 连接CD.
方法二:如图2,延长BC到 , 使得 , 连接AD.

我选择方法 ▲ .
证明:
22. 如图,在 和 中, , , .求证 .