2024年北师大版数学七年级下册单元清测试(第四章) 培优卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. △ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )A、35cm B、30cm C、45cm D、55cm2. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( )
 A、1个 B、2个 C、3个 D、4个3. 如图, ,则图中全等三角形共有( )
A、1个 B、2个 C、3个 D、4个3. 如图, ,则图中全等三角形共有( )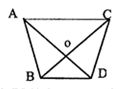 A、1对 B、2对 C、3对 D、4对4. 如图,已知.下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图中两三角形全等的依据是( )
A、1对 B、2对 C、3对 D、4对4. 如图,已知.下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图中两三角形全等的依据是( ) A、SAS B、SSS C、AAS D、ASA5. 如图,将长方形纸片ABCD沿对角线AC折叠后点B落在点E处,判断△EFA≌△DFC的依据是( )
A、SAS B、SSS C、AAS D、ASA5. 如图,将长方形纸片ABCD沿对角线AC折叠后点B落在点E处,判断△EFA≌△DFC的依据是( ) A、SAS B、ASA C、AAS D、HL6. 如图,已知方格纸中是4个相同的正方形,则( )
A、SAS B、ASA C、AAS D、HL6. 如图,已知方格纸中是4个相同的正方形,则( ) A、60° B、90° C、100° D、120°7. 已知的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( )
A、60° B、90° C、100° D、120°7. 已知的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( ) A、乙和丙 B、甲和乙 C、只有乙 D、只有丙8. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).
A、乙和丙 B、甲和乙 C、只有乙 D、只有丙8. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).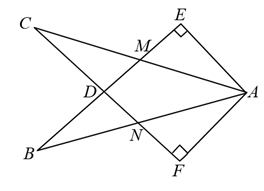 A、1个 B、2个 C、3个 D、4个9. 要得知某一池塘两端A,B的距离,发现其无法直接测量,两同学提供了如下间接测量方案.
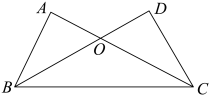
A、1个 B、2个 C、3个 D、4个9. 要得知某一池塘两端A,B的距离,发现其无法直接测量,两同学提供了如下间接测量方案.方案Ⅰ:如图1,先过点B作 , 再在上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测量的长即可;
方案Ⅱ:如图2,过点B作 , 再由点D观测,用测角仪在的延长线上取一点C,使 , 则测量的长即可.
对于方案Ⅰ、Ⅱ,说法正确的是( )
 A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行10. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行10. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )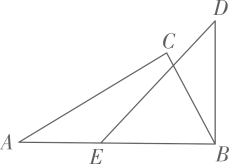 A、或或 B、或或 C、或或 D、或或
A、或或 B、或或 C、或或 D、或或二、填空题
-
11. 如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD、BE的交于点F,若BF=AC,CD=6,BD=8,则线段AF的长度为 .
 12. 如图,点在上,与相交于点 , ≌ , , , 则的度数为 度
12. 如图,点在上,与相交于点 , ≌ , , , 则的度数为 度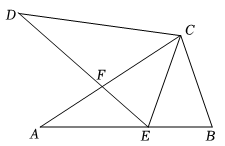 13. 如图,和的边相交于点O, . 添加一个条件,使得 . 这个条件可以是 . (填写所有符合要求的条件序号)
13. 如图,和的边相交于点O, . 添加一个条件,使得 . 这个条件可以是 . (填写所有符合要求的条件序号)①;②;③;④ .
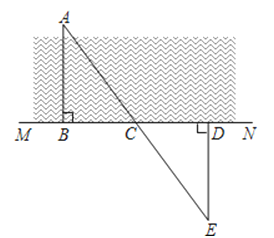
 14. 在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:
14. 在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:①在A点的对岸作直线MN;
②用三角板作AB⊥MN垂足为B;
③在直线MN取两点C、D,使 BC=CD;
④过D作DE⊥MN交AC的延长线于E,由三角形全等可知DE的长度等于河宽AB.
在以上的做法中,△ABC≌△DEC的根据是
 15. 如图,已知长方形中, , , 点在边上, , 点在线段上以的速度由点向点运动,到达点后马上折返,向点运动,点在线段上以的速度由C点向D点运动.点F、G同时出发,当一个点到达终点停止运动时,另一个点也随之停止运动,设运动的时间为t秒.若以E,B,F为顶点的三角形和以F,C,G为顶点的三角形全等,则t=秒.
15. 如图,已知长方形中, , , 点在边上, , 点在线段上以的速度由点向点运动,到达点后马上折返,向点运动,点在线段上以的速度由C点向D点运动.点F、G同时出发,当一个点到达终点停止运动时,另一个点也随之停止运动,设运动的时间为t秒.若以E,B,F为顶点的三角形和以F,C,G为顶点的三角形全等,则t=秒.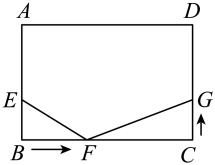 16. 如图,直线 , 一副三角板按如图1摆放,其中 , , . 保持三角板不动,现将三角板绕点以每秒的速度顺时针旋转,如图2,设旋转时间为t秒,且 , 则经过秒边与三角板的一条直角边(边 , )平行.
16. 如图,直线 , 一副三角板按如图1摆放,其中 , , . 保持三角板不动,现将三角板绕点以每秒的速度顺时针旋转,如图2,设旋转时间为t秒,且 , 则经过秒边与三角板的一条直角边(边 , )平行.
三、解答题
-
17. 如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
 (1)、求证:△BDE≌△CDF;(2)、若AE=13,AF=7,试求DE的长.18. 如图,在等边三角形中,点M为边上任意一点,延长至点N , 使 , 连接交于点P , 于点H .
(1)、求证:△BDE≌△CDF;(2)、若AE=13,AF=7,试求DE的长.18. 如图,在等边三角形中,点M为边上任意一点,延长至点N , 使 , 连接交于点P , 于点H . (1)、求证:;(2)、若 , 求线段的长.19. 如图,点在边上, , , .
(1)、求证:;(2)、若 , 求线段的长.19. 如图,点在边上, , , . (1)、求证:;(2)、∠ , , 求的度数.20. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上.
(1)、求证:;(2)、∠ , , 求的度数.20. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上. (1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.21. 如图,已知△BAC和△DAE的顶点A重合,∠BAC=∠DAE , AB=AC , AD=AE , 连接BD、CE交于点M .
(1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.21. 如图,已知△BAC和△DAE的顶点A重合,∠BAC=∠DAE , AB=AC , AD=AE , 连接BD、CE交于点M . (1)、证明:∠ABD=∠ACE;(2)、若∠BAC=70°,求∠BMC的大小.22. 已知:在和中, , .
(1)、证明:∠ABD=∠ACE;(2)、若∠BAC=70°,求∠BMC的大小.22. 已知:在和中, , .图1
 图2
图2 (1)、如图1,若 .
(1)、如图1,若 .①求证: . ②求的度数.
(2)、如图2,若 , 的大小为(直接写出结果,不证明).23. (1)、【模型启迪】如图1,在△ABC中,D为BC边的中点,连接AD并延长至点H , 使DH=AD , 连接BH , 则AC与BH的数量关系为 , 位置关系为 .(2)、【模型探索】如图2,在△ABC中,D为BC边的中点,连接AD , E为AC边上一点,连接BE交AD于点F , 且BF=AC . 求证:AE=EF .24. 综合与实践(1)、问题初探
(1)、【模型启迪】如图1,在△ABC中,D为BC边的中点,连接AD并延长至点H , 使DH=AD , 连接BH , 则AC与BH的数量关系为 , 位置关系为 .(2)、【模型探索】如图2,在△ABC中,D为BC边的中点,连接AD , E为AC边上一点,连接BE交AD于点F , 且BF=AC . 求证:AE=EF .24. 综合与实践(1)、问题初探如图1,在等腰直角△ABC中,∠B=90°,AB=BC,将△ABD沿着AD折叠得到△AED,AB的对应边AE落在AC上,点B的对应点为E,折痕AD交BC于点D.

求证:AC=AB+BD;
(2)、方法迁移如图2,AD是△ABC的角平分线,∠C=2∠B.求证:AB=AC+DC;
 (3)、问题拓展
(3)、问题拓展如图3,在△ABC中,∠ABC=2∠C,AD是△ABC的外角的平分线,交CB的延长线于点D.请你直接写出线段AC,AB,BD之间的数量关系.
