2024年北师大版数学七年级下册单元清测试(第四章) 基础卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. 在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )A、 B、 C、 D、2. 如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
 A、线段DE B、线段BE C、线段EF D、线段FG3. 如图,平面镜放置在水平地面上,墙面于点 , 一束光线照射到镜面上,反射光线为 , 点在上,若 , 则的度数为( )
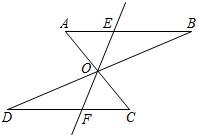
A、线段DE B、线段BE C、线段EF D、线段FG3. 如图,平面镜放置在水平地面上,墙面于点 , 一束光线照射到镜面上,反射光线为 , 点在上,若 , 则的度数为( ) A、 B、 C、 D、4. 如图, , cm, cm,则 的长为( )
A、 B、 C、 D、4. 如图, , cm, cm,则 的长为( ) A、4cm B、3cm C、2cm D、不能确定5. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A、4cm B、3cm C、2cm D、不能确定5. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )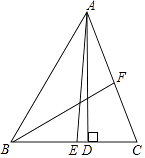 A、75° B、80° C、85° D、90°6. 如图,已知图中的两个三角形全等,则∠α的度数是( )
A、75° B、80° C、85° D、90°6. 如图,已知图中的两个三角形全等,则∠α的度数是( ) A、72° B、60° C、58° D、50°7. 如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( )
A、72° B、60° C、58° D、50°7. 如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( ) A、∠B=∠C B、AF∥DE C、AE=DE D、AB∥DC8. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A、∠B=∠C B、AF∥DE C、AE=DE D、AB∥DC8. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )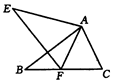 A、1个 B、2个 C、3个 D、4个9. 如图,下面选项中的两个三角形全等的是( )
A、1个 B、2个 C、3个 D、4个9. 如图,下面选项中的两个三角形全等的是( ) A、①② B、④③ C、③④ D、①④10. 如图,与都是等边三角形,且 , 下列结论:①;②;③;④若 , , 则 . 其中正确的是( )
A、①② B、④③ C、③④ D、①④10. 如图,与都是等边三角形,且 , 下列结论:①;②;③;④若 , , 则 . 其中正确的是( ) A、①② B、①③④ C、①②④ D、①②③④
A、①② B、①③④ C、①②④ D、①②③④二、填空题
-
11. 如图,AD=AE , ∠1=∠2,请你添加一个条件 (只填一个即可),使△ABD≌△ACE .
 12. 如图,在中, , 为边的中线,的周长与的周长相差3, , 则 .
12. 如图,在中, , 为边的中线,的周长与的周长相差3, , 则 . 13. 如图, , 若 , 则.
13. 如图, , 若 , 则. 14. 如图, , , 请你添加一个条件: , 使 . (写出一个条件即可)
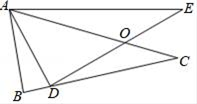
14. 如图, , , 请你添加一个条件: , 使 . (写出一个条件即可) 15. 如图,已知 , , , 在同一条直线上, , , , 若 , , 则 .
15. 如图,已知 , , , 在同一条直线上, , , , 若 , , 则 .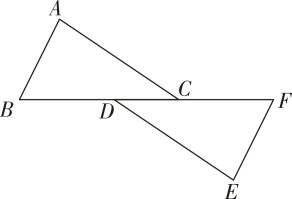 16. 在测量一个小口圆形容器的壁厚时,小明用“x型转动钳”按如图方法进行测量,其中 , 测得 , 圆形容器的壁厚是.
16. 在测量一个小口圆形容器的壁厚时,小明用“x型转动钳”按如图方法进行测量,其中 , 测得 , 圆形容器的壁厚是.
三、解答题
-
17. 如图,点A , B , C , D在同一直线上,AB=CD , AE∥DF , EC∥BF .
 (1)、求证:AE=DF;(2)、若AD=8,BC=2,求AC的长.18. 已知:如图,在和中,在同一条直线上.下面四个条件:
(1)、求证:AE=DF;(2)、若AD=8,BC=2,求AC的长.18. 已知:如图,在和中,在同一条直线上.下面四个条件:①②;③;④
 (1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.19. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.19. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E. (1)、求∠CBE的度数;(2)、过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.20. 如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 .
(1)、求∠CBE的度数;(2)、过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.20. 如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 . (1)、求证: ;(2)、若 , ,求 的度数.21. 如图, 是四边形 的对角线, ,点 , 分别在 , 上, , ,连接 .
(1)、求证: ;(2)、若 , ,求 的度数.21. 如图, 是四边形 的对角线, ,点 , 分别在 , 上, , ,连接 . (1)、求证: ;(2)、若 ∥ , ,求 的度数.22. 如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)、求证: ;(2)、若 ∥ , ,求 的度数.22. 如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E. (1)、求证:△BCE≌△CAD;(2)、若BE=5,DE=7,则△ACD的周长是.
(1)、求证:△BCE≌△CAD;(2)、若BE=5,DE=7,则△ACD的周长是.