2024年北师大版数学七年级下册周测卷(第四章 第3-5节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
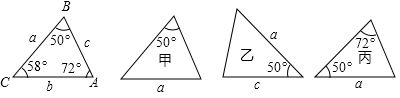 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙2. 如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙2. 如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )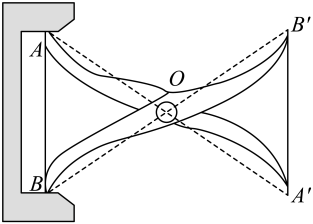 A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两余直线被一组平行线所截,所的对应线段成比例 D、两点之间线段最短3. 阅读以下作图步骤:
A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两余直线被一组平行线所截,所的对应线段成比例 D、两点之间线段最短3. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且4. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( )
A、且 B、且 C、且 D、且4. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( ) A、 B、 C、 D、5. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、5. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )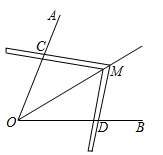 A、 B、 C、 D、6. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( )
A、 B、 C、 D、6. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( ) A、 B、 C、 D、7. 在中, , 点是边的中点,过点作于点 , 点是延长线上一点,已知 , 下列结论不一定正确的是( )
A、 B、 C、 D、7. 在中, , 点是边的中点,过点作于点 , 点是延长线上一点,已知 , 下列结论不一定正确的是( ) A、 B、 C、 D、8. 如图 ,要测量河两岸相对的两点 A,B的距离,先在 AB的垂线 BF上取两点 C,D,使 BC=CD,再作出 BF的垂线 DE,使点 A,C,E在同一条直线上(如图),可以说明△ABC≌△EDC,得 AB=DE,因此测得 DE的 长就是 AB的长,判定△ABC≌△EDC,最恰当的理由是( )
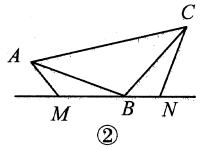
A、 B、 C、 D、8. 如图 ,要测量河两岸相对的两点 A,B的距离,先在 AB的垂线 BF上取两点 C,D,使 BC=CD,再作出 BF的垂线 DE,使点 A,C,E在同一条直线上(如图),可以说明△ABC≌△EDC,得 AB=DE,因此测得 DE的 长就是 AB的长,判定△ABC≌△EDC,最恰当的理由是( )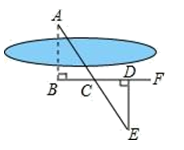 A、SAS B、HL C、SSS D、ASA9. 如图,在中,点E在延长线上,已知 , , , , , 则的度数是( )
A、SAS B、HL C、SSS D、ASA9. 如图,在中,点E在延长线上,已知 , , , , , 则的度数是( ) A、 B、 C、 D、10. 如图,在中, , , , 点为的中点,如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.若在某一时刻能使与全等.则点的运动速度为( )
A、 B、 C、 D、10. 如图,在中, , , , 点为的中点,如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.若在某一时刻能使与全等.则点的运动速度为( )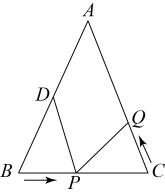 A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题
-
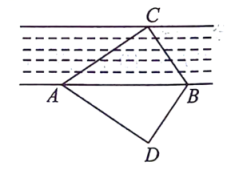
11. 某数学兴趣小组利用全等三角形的知识测试某小河的宽度,如图,点是小河两边的三点,在河边下方选择一点,使得 , 若测得米,的面积为30平方米,则点到的距离为米.
 12. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.
12. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.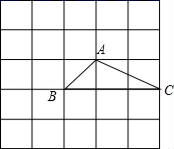 13. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .
13. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .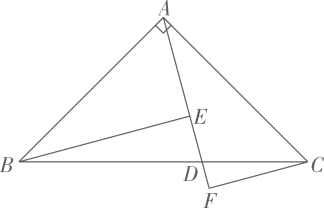 14. 如图,在四边形ABCD中,对角线AC,BD相交于点O, , 请你添加一个条件 , 使 .
14. 如图,在四边形ABCD中,对角线AC,BD相交于点O, , 请你添加一个条件 , 使 .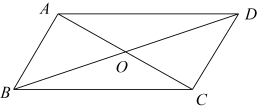 15. 如图,在 中, , ,点D是边AB上一点,点B关于直线CD的对称点为 ,当 时,则 的度数为 .
15. 如图,在 中, , ,点D是边AB上一点,点B关于直线CD的对称点为 ,当 时,则 的度数为 . 16. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE , 若DE=EF , CE=2,则AD的长为 .
16. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE , 若DE=EF , CE=2,则AD的长为 .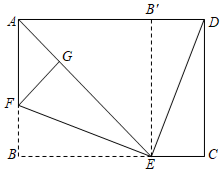
三、解答题
-
17. 如图,在中, , 作 , 且使 , 作 , 交的延长线于点求证: .
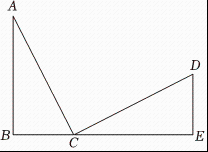 18. 如图,在和中,延长交于 , , . 求证: .
18. 如图,在和中,延长交于 , , . 求证: . 19. 已知:如图, , , . 求证: .
19. 已知:如图, , , . 求证: . 20. 如图, 是 的边 上一点, , 交 于 点, .
20. 如图, 是 的边 上一点, , 交 于 点, . (1)、求证: ≌ ;(2)、若 , ,求 的长.21. 如图, , , . , 与 交于点 .
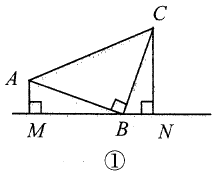
(1)、求证: ≌ ;(2)、若 , ,求 的长.21. 如图, , , . , 与 交于点 .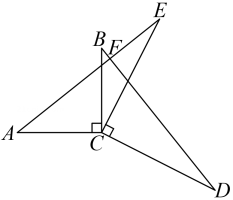 (1)、求证: ;(2)、求 的度数.22. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)、求证: ;(2)、求 的度数.22. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.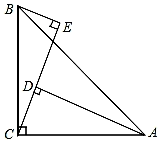 (1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.
(1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.