2024年北师大版数学七年级下册周测卷(第四章 第3-5节)基础卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 如图,等腰△ 中,点D , E分别在腰AB , AC上,添加下列条件,不能判定 ≌ 的是( )
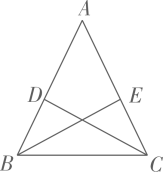 A、 B、 C、 D、2. 如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A、 B、 C、 D、2. 如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( ) A、∠A=∠D B、∠ACB=∠DBC C、AC=DB D、AB=DC3. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( )
A、∠A=∠D B、∠ACB=∠DBC C、AC=DB D、AB=DC3. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( ) A、SSS B、ASA C、SAS D、AAS4. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A、SSS B、ASA C、SAS D、AAS4. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) A、 B、 C、 D、5. 根据下列条件,不能画出唯一的是( )A、 , , B、 , , C、 , , D、 , ,6. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、 B、 C、 D、5. 根据下列条件,不能画出唯一的是( )A、 , , B、 , , C、 , , D、 , ,6. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、4个 B、3个 C、2个 D、1个7. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
A、4个 B、3个 C、2个 D、1个7. 如图是作△ABC的作图痕迹,则此作图的已知条件是( ) A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角8. 如图,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带上( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角8. 如图,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带上( )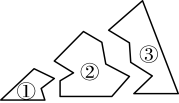 A、① B、② C、③ D、①和③9. 如图①是两位同学玩跷跷板的场景,如图②跷跷板示意图,支柱与地面垂直,点O是的中点,绕着点O上下转动.若A端落地时, , 则跷跷板上下可转动的最大角度(即)是( )
A、① B、② C、③ D、①和③9. 如图①是两位同学玩跷跷板的场景,如图②跷跷板示意图,支柱与地面垂直,点O是的中点,绕着点O上下转动.若A端落地时, , 则跷跷板上下可转动的最大角度(即)是( ) A、 B、 C、 D、10. 如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是( )
A、 B、 C、 D、10. 如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是( ) A、10米 B、20米 C、30米 D、40米
A、10米 B、20米 C、30米 D、40米二、填空题
-
11. 如图,AC=BC,请你添加一对边或一对角相等的条件,使AD=BE.你所添加的条件是 .
 12. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个)
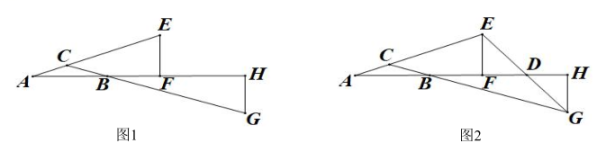
12. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个) 13. 如图,AC=DC,BC=EC,请你添加一个适当的条件: , 使得△ABC≌△DEC.
13. 如图,AC=DC,BC=EC,请你添加一个适当的条件: , 使得△ABC≌△DEC.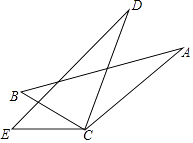 14. 如图,点E、C、F、B在一条直线上,EC=BF, , 当添加条件时,可由“角边角”判定△ABC≌△DEF.
14. 如图,点E、C、F、B在一条直线上,EC=BF, , 当添加条件时,可由“角边角”判定△ABC≌△DEF. 15. 如图所示的5个三角形中:△ABC≌ , △DEF≌ .
15. 如图所示的5个三角形中:△ABC≌ , △DEF≌ .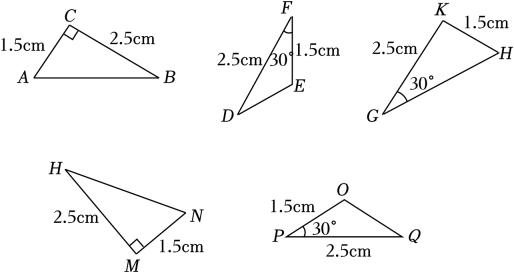 16. 在测量一个小口圆形容器的壁厚时,小明用“型转动钳”按如图方法进行测量,其中 , 测量的长度即可知道的长度.此方法用到了一个重要的和两个三角形有关的数学知识是;这个数学知识成立的依据是 .
16. 在测量一个小口圆形容器的壁厚时,小明用“型转动钳”按如图方法进行测量,其中 , 测量的长度即可知道的长度.此方法用到了一个重要的和两个三角形有关的数学知识是;这个数学知识成立的依据是 .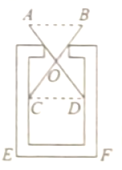
三、解答题
-
17. 已知:如图,D是BC上一点,AB=BD,DE∥AB,∠A=∠DBE.
求证:AC=BE.
 18. 小明利用一根3m长的竿子来测量路灯的高度.他的方法是这样的:在路灯前选一点 , 使m,并测得 , 然后把竖直的竿子(m)在的延长线上移动,使 , 此时量得m.根据这些数据,小明计算出了路灯的高度.你知道小明计算的路灯的高度是多少?为什么?
18. 小明利用一根3m长的竿子来测量路灯的高度.他的方法是这样的:在路灯前选一点 , 使m,并测得 , 然后把竖直的竿子(m)在的延长线上移动,使 , 此时量得m.根据这些数据,小明计算出了路灯的高度.你知道小明计算的路灯的高度是多少?为什么? 19. 已知:如图,∠C=∠D=90°,AC=AD.求证:
19. 已知:如图,∠C=∠D=90°,AC=AD.求证: (1)、∠ABC=∠ABD.(2)、BC= BD.20. 如图,AB∥CD , AB=CD , 点E和点F在线段BC上,∠A=∠D .
(1)、∠ABC=∠ABD.(2)、BC= BD.20. 如图,AB∥CD , AB=CD , 点E和点F在线段BC上,∠A=∠D . (1)、求证:AE=DF .(2)、若BC=16,EF=6,求BE的长.21. 如图,已知点B、D、E、C四点在一条直线上,且△ABE≌△ACD.
(1)、求证:AE=DF .(2)、若BC=16,EF=6,求BE的长.21. 如图,已知点B、D、E、C四点在一条直线上,且△ABE≌△ACD.
求证
(1)、BD=CE;(2)、△ABD≌△ACE.