2024年北师大版数学七年级下册周测卷(第四章 第1-3节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 一个木工师傅现有两根木条,它们的长度分别为30和80,现在要做一个三角形的木架,则第三根木条应选取( )A、10 B、70 C、130 D、402. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
 A、10° B、15° C、18° D、30°3. 下列说法错误的是( )
A、10° B、15° C、18° D、30°3. 下列说法错误的是( )
A、三角形的中线、高、角平分线都是线段 B、任意三角形内角和都是180° C、三角形按角可分为锐角三角形、直角三角形和等腰三角形 D、直角三角形两锐角互余4. 在△ABC中,画出边AC上的高,画法正确的是( )
A、 B、
B、 C、
C、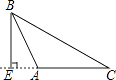 D、
D、 5. 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )
5. 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )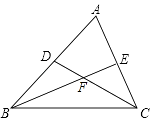 A、51° B、52° C、53° D、58°6. 下列说法正确的是( )
A、51° B、52° C、53° D、58°6. 下列说法正确的是( )
A、全等三角形是指形状相同的三角形 B、全等三角形是指面积相等的两个三角形 C、全等三角形的周长和面积相等 D、所有等边三角形是全等三角形7. 如图,强强想测量旗杆的高度,旗杆对面有一高为米的大楼 , 大楼与旗杆相距米(米),在大楼前米的点P处,测得 , 且 , , 则旗杆的高为( ) A、8米 B、米 C、米 D、米8. 中,厘米, , 厘米,点为的中点.如果点在线段上以厘米/秒的速度由点向点运动,同时,点在线段上由点向点运动.若点的运动速度为厘米/秒,则当与全等时,的值为( )
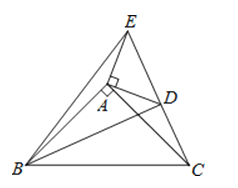
A、8米 B、米 C、米 D、米8. 中,厘米, , 厘米,点为的中点.如果点在线段上以厘米/秒的速度由点向点运动,同时,点在线段上由点向点运动.若点的运动速度为厘米/秒,则当与全等时,的值为( ) A、 B、 C、或 D、或9. 已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
A、 B、 C、或 D、或9. 已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
 A、1 B、2 C、3 D、410. 在中, , , 是边上的中线,则的取值范围是( )
A、1 B、2 C、3 D、410. 在中, , , 是边上的中线,则的取值范围是( )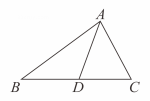 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定二、填空题
-
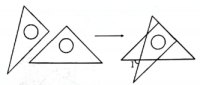
11. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则度.
 12. 已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .13. 如图,为的中线, , , 若的周长28cm,则的周长为.
12. 已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .13. 如图,为的中线, , , 若的周长28cm,则的周长为. 14. 已知≌ , 且的周长为 , 若 , , .15. 如图所示,△ABD≌△EBC,则下列结论:①CD⊥AE;②AD⊥CE;③
14. 已知≌ , 且的周长为 , 若 , , .15. 如图所示,△ABD≌△EBC,则下列结论:①CD⊥AE;②AD⊥CE;③∠EAD=∠ECD.其中正确的有(只填序号).
 16. 如图,点在同一直线上, , 添加条件: , 则可用证明 .
16. 如图,点在同一直线上, , 添加条件: , 则可用证明 .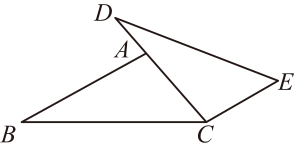
三、解答题
-
17. 如图,在中,于点D , 平分 .
 (1)、若 , 求的度数;(2)、若 , , 求的度数(用含、的式子来表示).18. 如图,三点在同一条直线上,且.
(1)、若 , 求的度数;(2)、若 , , 求的度数(用含、的式子来表示).18. 如图,三点在同一条直线上,且. (1)、若 , , 求的长;(2)、若 , 求的度数.19. 如图,如图,点P在AB上,∠1=∠2, ∠3=∠4.
(1)、若 , , 求的长;(2)、若 , 求的度数.19. 如图,如图,点P在AB上,∠1=∠2, ∠3=∠4.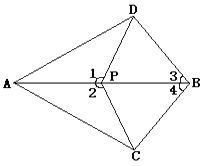 (1)、求证: △BDP≌△BCP;(2)、求证:AD=AC.20. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .
(1)、求证: △BDP≌△BCP;(2)、求证:AD=AC.20. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .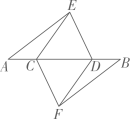 (1)、求证:;(2)、若 , , 求的长.21. 如图,BE平分△ABC的内角∠ABC,CE平分△ABC 的外角. , BE,CE 相交于点 E.
(1)、求证:;(2)、若 , , 求的长.21. 如图,BE平分△ABC的内角∠ABC,CE平分△ABC 的外角. , BE,CE 相交于点 E. (1)、若∠ABC=40°,∠ACB=80°,求∠E 的度数;(2)、若∠ABC+∠ACB=100°,求∠E的度数.22. 如图,在中,点D为的平分线BD上一点,连接AD,过点D作交AB于点E,交AC于点F.
(1)、若∠ABC=40°,∠ACB=80°,求∠E 的度数;(2)、若∠ABC+∠ACB=100°,求∠E的度数.22. 如图,在中,点D为的平分线BD上一点,连接AD,过点D作交AB于点E,交AC于点F.
 (1)、如图1,若于点D, , 求的度数;(2)、如图2,若 , , 求的度数(用含和的代数式表示).23. 如图,AB=8cm,∠A=∠B=60°,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以xcm/s的速度由点B向点D运动,它们运动的时间为t(s).问:
(1)、如图1,若于点D, , 求的度数;(2)、如图2,若 , , 求的度数(用含和的代数式表示).23. 如图,AB=8cm,∠A=∠B=60°,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以xcm/s的速度由点B向点D运动,它们运动的时间为t(s).问: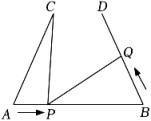 (1)、AP= , BP= , BQ=(用含x或t的代数式表示);(2)、当运动时间t为何值时,△ACP与△BPQ全等.24. 在中,平分 , .
(1)、AP= , BP= , BQ=(用含x或t的代数式表示);(2)、当运动时间t为何值时,△ACP与△BPQ全等.24. 在中,平分 , .
图1 图2 图3
(1)、如图1,若于点 , , , 则;(2)、如图2,若点是线段上一动点,过点作于点 , 则与 , 之间的数量关系是;(3)、如图3,若点是延长线上一点,过点作于点 , 则与 , 之间有何数量关系?画出图形并证明你的结论.