2024年北师大版数学七年级下册单元清测试(第三章) 培优卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
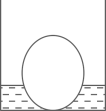
1. 下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
 A、
A、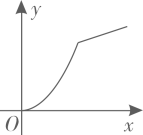 B、
B、 C、
C、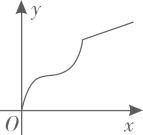 D、
D、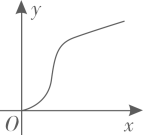 2. 如图能反映小亮同学参加1000米跑体能测试中,脉搏和耗氧量变化的曲线是( )
2. 如图能反映小亮同学参加1000米跑体能测试中,脉搏和耗氧量变化的曲线是( )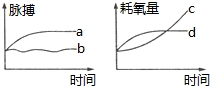 A、a和c B、a和d C、b和c D、b和d3. 一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )A、y=x(15-x) B、y=x(30-x) C、y=x(30-2x) D、y=x(15+x)4. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )
A、a和c B、a和d C、b和c D、b和d3. 一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )A、y=x(15-x) B、y=x(30-x) C、y=x(30-2x) D、y=x(15+x)4. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )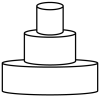 A、
A、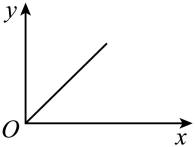 B、
B、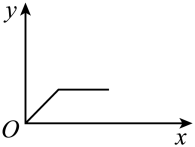 C、
C、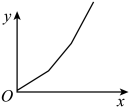 D、
D、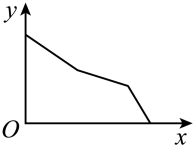 5. 弹簧挂上物体后会伸长,测得一弹簧的长度最长为 , 与所挂的物体的质量间有下面的关系:
5. 弹簧挂上物体后会伸长,测得一弹簧的长度最长为 , 与所挂的物体的质量间有下面的关系:x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法中不正确的是( )
A、与都是变量 B、所挂物体质量为时,弹簧长度为 C、弹簧不挂重物时的长度为 D、物体质量每增加 , 弹簧长度增加6. 妈妈从家里出发去公园锻炼,她连续匀速走了后回到家,如图,图中的折线段是她出发后所在位置离家的距离与行走时间之间的关系,则下列图形中可以大致描述妈妈行走的路线的是( )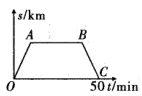 A、
A、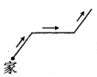 B、
B、 C、
C、 D、
D、 7. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )
7. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )木板的支撑物高度
…
下滑时间
…
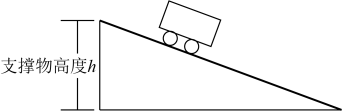 A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短8. 以下四种情境分别描述了两个变量之间的关系:
A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短8. 以下四种情境分别描述了两个变量之间的关系: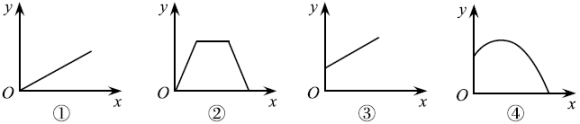
甲:运动员推铅球时,铅球的高度与水平距离的关系;
乙:食堂需购买一批餐具,支付费用与购餐具的数量的关系;
丙:一长方形水池里原有部分水,再匀速往里注水,水池中水面的高度与注水时间的关系;
丁:小明周末离家去看电影,结束后,原速度原路返回,小明离家的距离与时间的关系.
用下面的图象刻画上述情境,排序正确的是( )
A、③①④② B、④③①② C、④①③② D、③①②④9. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:支撑物的高度
10
20
30
40
50
60
70
小车下滑的时间
4.23
3.00
2.45
2.13
1.89
1.71
1.59
下列说法正确的是( )
A、t是自变量,h是因变量 B、h每增加 , t减小1.23 C、随着h逐渐变大,t也逐渐变大 D、随着h逐渐升高,小车下滑的平均速度逐渐加快10. 佳佳和爸爸一起从家出发,匀速行走后抵达离家的报亭,佳佳随即按原速返回,爸爸看了10min报后返回,恰好与佳佳同时到家.则表示爸爸离家后距离与时间关系的大致图象是( )A、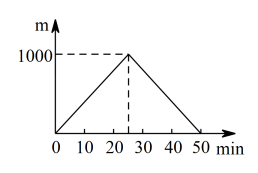 B、
B、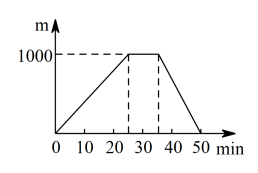 C、
C、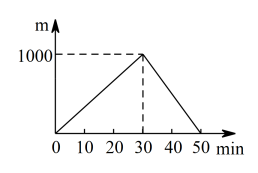 D、
D、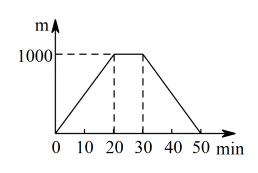
二、填空题
-
11. 观察下列图形及表格:
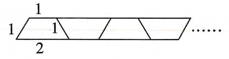
梯形个数
1
2
3
4
5
6
周长
5
8
11
14
17
20
则周长与梯形个数之间的关系式为.
12. 为了解某品牌汽车的耗油量,人们对这种车在高速公路上做了耗油试验,并把试验的数据记下来,制成下表:汽车行驶时间
邮箱剩余油量
根据上表的数据,写出与的关系式: .
13. 小颖准备乘出租车到距家超过3km的科技馆参观,出租车的收费标准如下:里程数/km
收费/元
3km以内(含3km)
8.00
3km以外每增加1km
1.80
则小颖应付车费y(元)与行驶里程数x(km)之间的关系式为.
14. 小明早上步行去车站,然后坐车去学校.如图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是 . (填序号)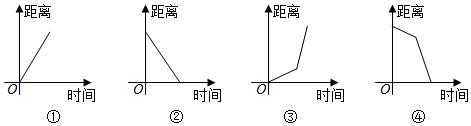 15. 如图,在中,边长为10,边上的高为6,点在上运动,设长为 , 则的面积与之间的关系式 .
15. 如图,在中,边长为10,边上的高为6,点在上运动,设长为 , 则的面积与之间的关系式 .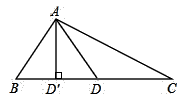 16. 某图书馆对外出租书的收费方式是:每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租后x天后,所收租金y与天数x的表达式为 .
16. 某图书馆对外出租书的收费方式是:每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租后x天后,所收租金y与天数x的表达式为 .三、解答题
-
17. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分,由于业务多,小明的爸爸打电话已超出了包月费.
下表是超出部分国内拨打的收费标准
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的表达式是什么?
(3)如果打电话超出25分钟,需付多少电话费?
(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
18. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示: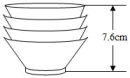
数量/只
1
2
3
4
5
…
高度/cm
4
5.2
6.4
7.6
8.8
…
(1)、上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)、用h(cm)表示这摞碗的高度,用x(只)表示这摞碗的数量,请用含有x的代数式表示h;(3)、若这摞碗的高度为 11.2cm,求这摞碗的数量.19. 如图,在梯形中, , , 高 , 点为边上任意一点,连接 , 当的长度由小到大变化时,四边形的面积也随之发生变化.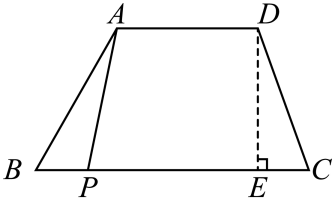 (1)、在这个变化过程中,自变量、因变量分别是什么?(2)、若设 , 四边形的面积为 , 求与之间的关系式;(3)、当时,求四边形的面积.20. 如图是一位病人的体温记录图,看图回答下列问题:
(1)、在这个变化过程中,自变量、因变量分别是什么?(2)、若设 , 四边形的面积为 , 求与之间的关系式;(3)、当时,求四边形的面积.20. 如图是一位病人的体温记录图,看图回答下列问题: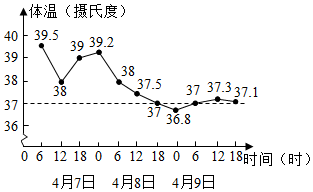 (1)、自变量是 , 因变量是;(2)、护士每隔小时给病人量一次体温;(3)、这位病人的最高体温是摄氏度,最低体温是 摄氏度;(4)、他在4月8日12时的体温是 摄氏度;(5)、图中的横虚线表示的含义.21. 一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表:
(1)、自变量是 , 因变量是;(2)、护士每隔小时给病人量一次体温;(3)、这位病人的最高体温是摄氏度,最低体温是 摄氏度;(4)、他在4月8日12时的体温是 摄氏度;(5)、图中的横虚线表示的含义.21. 一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表:时间(秒)
0
1
2
3
4
5
6
7
8
9
10
速度(米/秒)
0
0.3
1.3
2.8
4.9
7.6
11.0
14.1
18.4
24.2
28.9
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用T表示时间,V表示速度,那么随着T的变化,V的变化趋势是什么?(3)、当T每增加1秒,V的变化情况相同吗?在哪1秒钟,V的增加最大?(4)、若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.22. “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.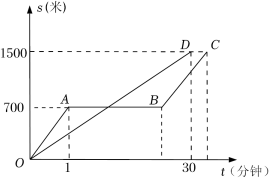 (1)、折线表示赛跑过程中的路程与时间关系,线段表示赛跑过程中的路程与时间的关系.(填“乌龟”和“兔子”)赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以800米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算一算兔子中间停下睡觉用了多少分钟?
(1)、折线表示赛跑过程中的路程与时间关系,线段表示赛跑过程中的路程与时间的关系.(填“乌龟”和“兔子”)赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以800米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算一算兔子中间停下睡觉用了多少分钟?